A circular disk radius R rotates with the constant angular velocity Ω. A point P moves along a straight guide; its distance from the center of the disk is given by ξ = R sin ω t where ω = const in given figure Determine the velocity and the acceleration of P
We use polar coordinates r ϕ to solve the problem. From Ω = const we findThe position vector is written as r = ξer → r = R sin ωterDifferentiation yields the velocity vectorv = ˙ξer + ξϕ˙ eϕ → v = Rω cos ωter + RΩ sin ωt eϕand the acceleration vector a = ¨ξ − ξϕ2 er + ξϕ¨ + 2 ˙ξϕ˙ e→ a = −Rω2 + Ω2 sin ωter + 2RωΩ cosωt eϕThe paths of point P are displayed for several values of Ω/ω in the following figures.
Related Solutions
A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in figure. The magnitude of acceleration of point P at an instant when its linear velocity is v and angular velocity is ω will be:
View SolutionThe value of (1−ω+ω^2 )^ 5 +(1+ω−ω^ 2 )^ 5 where ω and ω^ 2 are the complex cube roots of unity, is
View SolutionIf are connected in parallel, what will be the current through the resistor?
View SolutionAn alternating current is given by 1 = 1 1 cos ω t + 1 2 sin ω t . sinomega t .The value of rms current is
View Solutioni) (1 + ω) (1 + ω ^ 4) (1 + ω ^ 8) = -ω ^ 2
View SolutionIn the following circuit the equivalent resistance between A and B is
10 Ω
20 Ω
30 Ω
40 Ω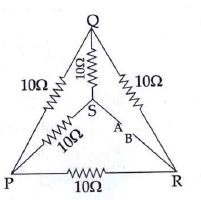
View SolutionA cylinder of water, is rotating about its own axis with uniform angular velocity ω. The shape of free surface of water will be
View Solutionत्रिज्या R की एक समान वृत्ताकार डिस्क से त्रिज्या R/4 की एक समाक्ष छोटी वृत्ताकार डिस्क काट ली गई है। यदि सम्पूर्ण डिस्क का केंद्र O हो तो शेष डिस्क के द्रव्यमान केंद्र की O से दूरी होगी
View SolutionThe average speed of a particle in S.H.M of amplitude A and angular velocity (ω) is
View Solutionइकाई के घन मूल #!# &
View SolutionConsider a disk of mass m , radius R lying on a liquid layer of thickness T and coefficient of viscosity eta as shown in the fig. The torque required to rotate the disk at a constant angular velocity Omega given the viscosity is uniformly eta .
View SolutionA circular disk of radius 2.0 m rotates, starting from rest, with a constant angular acceleration of . What is the tangential acceleration of a point on the edge of the disk at the instant that its angular speed is 1.0 rev/s?
View SolutionReading of ammeter is 2A. Find value of R (in Ω).
View SolutionWhat is the effective resistance (in Ω) of two resistors 21 Ω and 28 Ω connected in parallel?
View Solutionएक पतली वृत्ताकार चकती जिसका द्रव्यमान M तथा त्रिज्या r है, अपने अक्ष के अनुदिश नियत कोणीय वेग से घूर्णन कर रही है। दो वस्तुएँ जिनमें प्रत्येक का द्रव्यमान m है, चकती के व्यास के दोनों सिरों से मृदुलता से जुड़ी हैं। अब चकती जिस कोणीय वेग से घूर्णन करेगी वह है
View SolutionR त्रिज्या की एक वृत्ताकार डिस्क को 2R त्रिज्या की एक बड़ी वृत्ताकार डिस्क से इस प्रकार काटा जाता है कि दोनों डिस्क की परिधि संपाती हो। नयी डिस्क के द्रव्यमान केन्द्र की बड़ी डिस्क के द्रव्यमान केन्द्र से दूरी का मान है
View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity omega in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
View SolutionA uniform disk of mass is rotating freely about a vertical axis through its centre with constant angular velocity A boy of mass starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity omega . A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA circular disk of radius 0.010 m rotates with a constant angular speed of 5.0 rev/s. What is the acceleration of a point on the edge of the disk?
View Solution