A bowling ball mass m moves with constant ve- locity v0 on the frictionless return of a bowling alley. It is lifted on a circular path radius r to the height 2r at the end of the return. The upper part of the circular path has a frictionless guide of length r ϕG Given the angle ϕG determine the velocity v0 such that the bowling ball reaches the upper level.
The velocity v0 has to be large enough so that the bowling ball reaches the upper level height 2r with a velocity v ≥ 0. It is convenient to use the Conservation of Energy Law to determine the relation between v0 and v. With 0 = mv20/2 V0 = 0 This yields a first requirement on v0In addition the velocity v0 has to be large enough so that the normal force between the bowling ball and the lower part of the circular path does not become zero before the ball reaches the guide of length rϕG. The necessary velocity vϕG follows from the equation of motion in the normal direction note that ϕ is measured from the upper level:The condition N ≥ 0 for ϕ = ϕG leads toIn order to calculate the corresponding velocity v0 we use the Conservation of Energy Law between the lower level and the beginning of the guide:T0 + V0 = T2 + V2Thus we obtain the second requirementBoth requirements are plotted in the figure which shows that the minimum velocity v0 is obtained as
Related Solutions
R त्रिज्या का एक अर्द्ध गोलाकार कटोरा एक क्षैतिज मेज पर रखा है। एक r त्रिज्या का छोटा गोला कटोरे में उसके उच्चतम बिन्दु पर रखते हैं तथा तब ही यह चलने लगता है। गोला बिना फिसले लुढ़कता है। निम्नतम बिन्दु पर इसका वेग है
View SolutionA small ball is pushed from a height h along a smooth hemispherical bowl of radius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
View SolutionWhat is the work done in upturning a thin hemispherical bowl as shown in the figure. The mass of the bowl is M and the radius of the bowl is R.
View SolutionA semicircular bowl of radius R is symmetrical to the axis that is rotating vertically relative to it. The ball placed in the bowl rotates without slipping on the surface of the bowl itself. If the surface of the bowl is smooth and the angle formed by the radius from the ball with the hoist alpha The bowl is completing
View SolutionA small ball is pushed from a height h along a smooth hemispherical bowl of rodius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
View Solutionद्रव्यमान m की एक वस्तु त्रिज्या R वाले अर्द्धगोलीय प्याले के धरातल पर इसके किनारे से नीचे की ओर सरकती है | प्याले की तली पर पहुँचने पर वस्तु का वेग होगा :
View SolutionA bowling machine projects a ball of mass 0.15kg in upward direction. If ball displaced along bowling machine 0.2 m and released. after released from bowling machine ball attain 20 m height then find force exerted by bowling machine on ball
View SolutionA bowling machine projects a ball of mass 0.15kg in upward direction. If ball displaced along bowling machine 0.2 m and released. after released from bowling machine ball attain 20 m height then find force exerted by bowling machine on ball
View SolutionIf the coefficient of friction between the worm and the bowl mu If the radius of the bowl is r then the maximum height where the bugs can crawl into the bowl
View Solution
A small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
View SolutionA small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
View SolutionA hemispherical bowl of radius R is rotating with respect to its axis of symmetry which is vertical. The ball placed in the bowl rotates along with the bowl without slipping on its surface. If the surface of the bowl is smooth and the angle made by the radius with the vertical alpha then find the angular speed with which the bowl is rotating.
View SolutionA ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (theta=0^(@)) of the path is v_(0) find the force of the path on the ball as a function of theta .
View SolutionA ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (theta=0^(@)) of the path is v_(0) find the force of the path on the ball as a function of theta .
View SolutionThere is a hemispherical bowl of radius R. A block of mass m slides from the rim of the bowl to the bottom. The acceleration of block at the bottom is
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
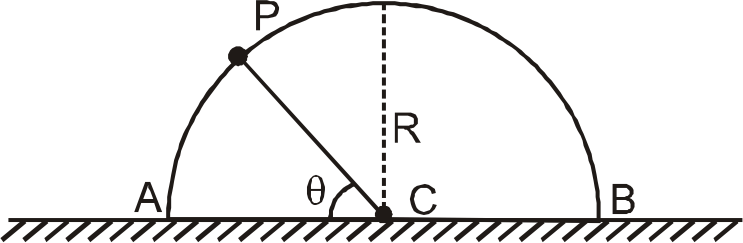
When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.

When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :
View SolutionSuppose a golf ball is hurled at a heavy bowling ball initially at rest and bounces elastically from the bowling ball after the collision
View SolutionA ball of radius r is made to oscillate in a bowl of radius R. Find the time period of oscillation.
View SolutionA ball of radius r is made to oscillate in a bowl of radius R, find its time period of oscillation.
View Solution