Two point masses P1 and P2 start at point A with zero initial velocities and travel on a circular path. P1 moves with a uniform tangential acceleration at1 and P2 moves with a given uniform angular velocity ω2. a What value must at1 have in order for the two masses to meet at point B?b What is the angular velocity of P1 at B? c What are the normal accelerations of the two masses at B?
The velocity and position of P1 follow from at1 = const = v˙ with the initial conditions s01 = 0 and v01 = 0 asSimilarly for point P2 we obtain from at2 = 0 with s02 = 0 and v02 = rω2:v2 = rω2 s2 = rω2ta Both points meet at time tB at point B thusThis leads tob The tangential acceleration at1 and the time tB are now known. Hence we can calculate the angular velocity of P1 at Bc The normal accelerations at B follow from an = rω2
Related Solutions
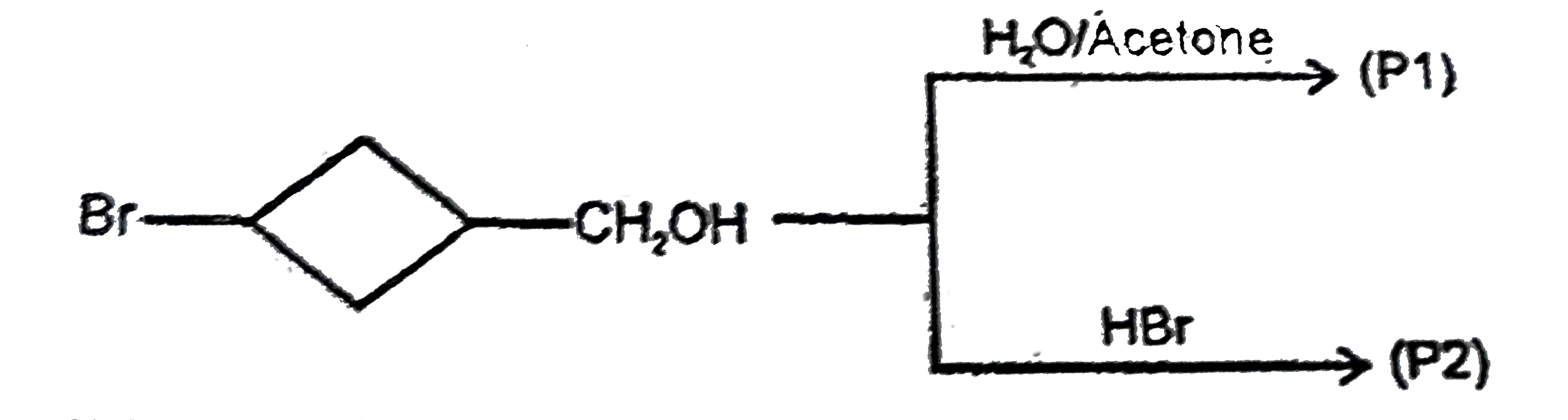
P1 and P2 are respectively
View SolutionP1 and P2 are respectively :
View SolutionProperties of ITF#!#P1 & P2
View SolutionA body A moves with a uniform acceleration a and zero initial velocity. Another body B, starts from the same point moves in the same direction with a constant velocity v. The two bodies meet after a time t. The value of t is
View SolutionA body A moves with a uniform acceleration a and zero initial velocity. Another body B starts from the same point, moves in the same direction with a constant velocity v. The two bodies meet after a time t. The value of t is
View SolutionThe pressure and density of a gas (Ƴ =5/3) changes adiabatically from (p1,d1 ) to (p2,d2).If d2/d1=27 the find value of p2/p1 ?
View SolutionA cylindrical tube with its base as shown is filled with water. It is moving down with a constant acceleration a along a fixed inclined plane with angle theta = 45^0 P1 and P2 are pressure points 1 and 2 resp located at base of tube. Let beta = (P1 - P2)/(rho g d) . Which statement is true?
View SolutionConsider the following events: : Six fair dices are rolled and at least one die shows six. : Twelve fair dice are rolled and at least two dice show six. Let be the probability of and be the probaility of . Which of the following is true? (A) p1 > p2 (B) p1 = p2 = 0.6651 (C) p1 < p2 (D) p1 = p2 = 0.3349
View SolutionA particle moving in a circular path of certain radius, with uniform angular velocity has an angular acceleration equal to :
View SolutionA particle is moving along a circular path of radius 'r' with uniform angular velocity omega . Its angular acceleration is
View Solution= 113400 இங்கு p1, p2, p3, p4 என்பன ஏறு வரிசையில் அமைந்த பகா எண்கள் மற்றும் x1, x2, x3, x4 என்பன முழுக்கள் எனில் p1, p2, p3, p4 மற்றும் x1, x2, x3, x4 ஆகியவற்றின் மதிப்புகளைக் காண்க.
View SolutionA body moving with uniform acceleration has velocities 20 ms and 30 ms when passing two points A and B. The velocity mid-way between A and B is:
View Solutionप्रारंभिक वेग शून्य ओर एकसमान त्वरण a के साथ एक पिण्ड A चलता है उसी बिन्दु से दूसरा पिण्ड B उसी दिशा में एकसमान वेग v से चलता है दोनों पिण्डो के मिलने में लगा समय होगा
View SolutionFrom power prove that for lens. P=P1+P2+P3+.........Pn
View SolutionTwo cars and cross a point with velocities and . After that they move with different uniform accelerations and the car overtakes with a speed of . What is velocity of at that instant?
View SolutionTwo cars A and B cross a point P with velocities 10m//s and 15m//s . After that they move with different uniform accelerations and the car A overtakes B with a speed of 25ms^(-1) . What is velocity of B at that instant?
View SolutionA car starts from rest and moves with uniform acceleration 'a' .At the same point a bike crosses with a uniform velocity 'u'.
When and where will they meet ?What is the velocity of car with respect to the bike at the time of meeting?
View SolutionA car starts from rest and moves with uniform acceleration , At the same instant from the same point a bike crosses with a uniform velocity . When and there will they meet ? What is the velocity of car with respect to the bike at the time of meeting?
View SolutionA car starts from rest and moves with uniform acceleration 'a'. At the same instant from the same point a bike crosses with a uniform velocity 'u'. When and where will they meet? What is the velocity of car with respect to the bike at the time of meeting?
View SolutionA car starts from rest and moves with uniform acceleration 'a', At the same instant from the same point a bike crosses with a uniform velocity 'u'. When and where will they meet ? What is the velocity of car with respect to the bike at the time of meeting?
View Solution