Find the direction of the velocity of a body sliding down the prism see preceding example when the latter is free to move. The mass of the sliding body is m the mass of the prism is M. The prism moves in a horizontal direction only under the action of the force exerted by the body. There is no friction.
Answer:Explanation:We denote by u the velocity of the prism Fig. 214 by vx and vy the horizontal and vertical components of the velocity v of the body relative to the ground and by β the angle betweentanβ = vy/vz. 1Since there acts on the prism in the vertical direction apart from the force from the body a force due to the reaction from the support then in considering the behaviour of the system of the body and the prism we may apply the law of conservation of momentum only to the horizontal component of the velocities of the body and the prism. Thus the velocities u and v0 satisfy the relation Mu = mvx . 2We assume that at some instant the body is at point A on the prism Fig. 215. During the next second the prism will move u cm to the left the body will move vx cm to the right in the horizontal direction vx and vy cm in the vertical direction. The magnitudesof these displacements should be such that the body will be at some point B. Consequently velocities vx and vy should satisfy not only the laws of conservation of energy and momentum but also the relationThis relation is an expression of the condition that the body always remains in contact with the prism during the motion. From relation 2 we findu = m/Mvx.Inserting the value of u into equation 3 making use of equation 1 and rearranging we obtainAs should have been expected tanβ > tanα and β > α. The velocity of a body sliding down a moving prism is directed at a larger angle to the horizontal than in the case of a stationary prism. Using the law of conservation of energy and knowing the height of the initial position of the body we can calculate the magnitudes of the velocities u and v.
Related Solutions
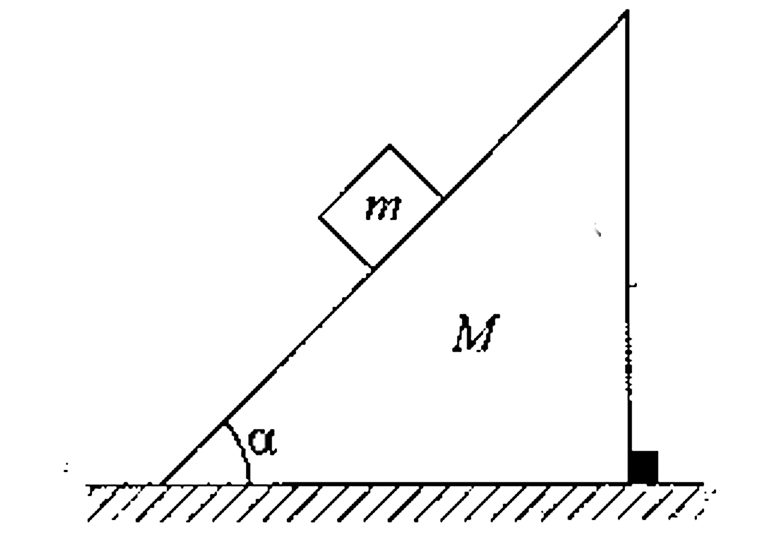
A heavy mass m slides down a triangular prism of mass M . The prism lies on a horizontal surface and can move along it without friction . What will be the direction of motion of m if the inclination of the hypotenuse of the prism is with the horizontal ?
View SolutionA prism of mass M is placed on a horizontal surface. A block of mass m slides on the prism, which in tum slides on the horizontal surface. Assuming all surfaces to be frictionless, find the acceleration of block with respect to prism.

View SolutionA prism of mass M is placed on a horizontal surface. A block of mass m slides on the prism, which in tum slides on the horizontal surface. Assuming all surfaces to be frictionless, find the acceleration of block with respect to prism.

View SolutionA prism of mass M is placed on a horizontal surface . A block of mass m slides on the prism , which in turn slides on the horizontal surface . Assuming all surfaces to be frictionless find the acceleration of block with respect to prism .
View SolutionWhat is the direction of frictional force actiog on a body moving or sliding towards east ?
View SolutionWhat is the direction of frictional force actiog on a body moving or sliding towards east ?
View SolutionA body with a mass m slides along the surfac of a trihedral prism of mass M, whose upper plane is inclined at an angle to the horizontal. The prism rests on a horizontal plane having a vertical ledge at the rear edge of the prism to keep it at rest as show in figure-2.69. Find the force exerted by the base of the prism on the plane ? Also find the force exerted by ledge on prism.
View SolutionThe mass m is placed on a body of mass M. There is no friction. The force F is applied on M on it moves with acceleration a. Then, the force on the top body is
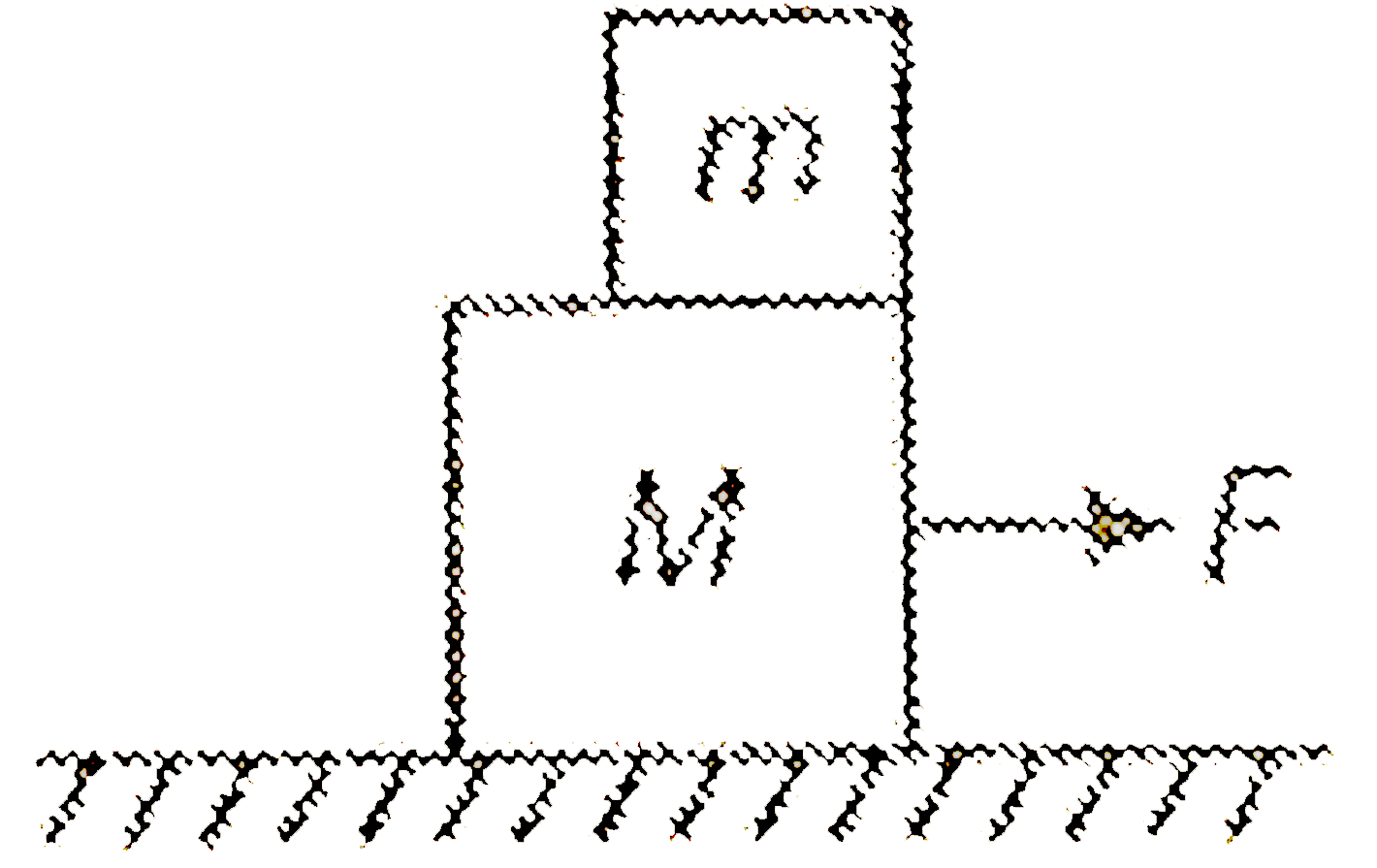
View SolutionA body with mass 'm' slides on the surface of a trihedral prism of mass M, whose upper plane is inclined at an angle theta to the horizontal. The prism rests on a horizontal plane having a vertical wall at the rear edge of the prism to keep it at rest. The normal reaction on the block is
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with ceefficeinet of friction |t. A horizontal force F is applied on the prism as shown. If the coefficeient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is:
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction mu . A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction mu . A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction mu . A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction . A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
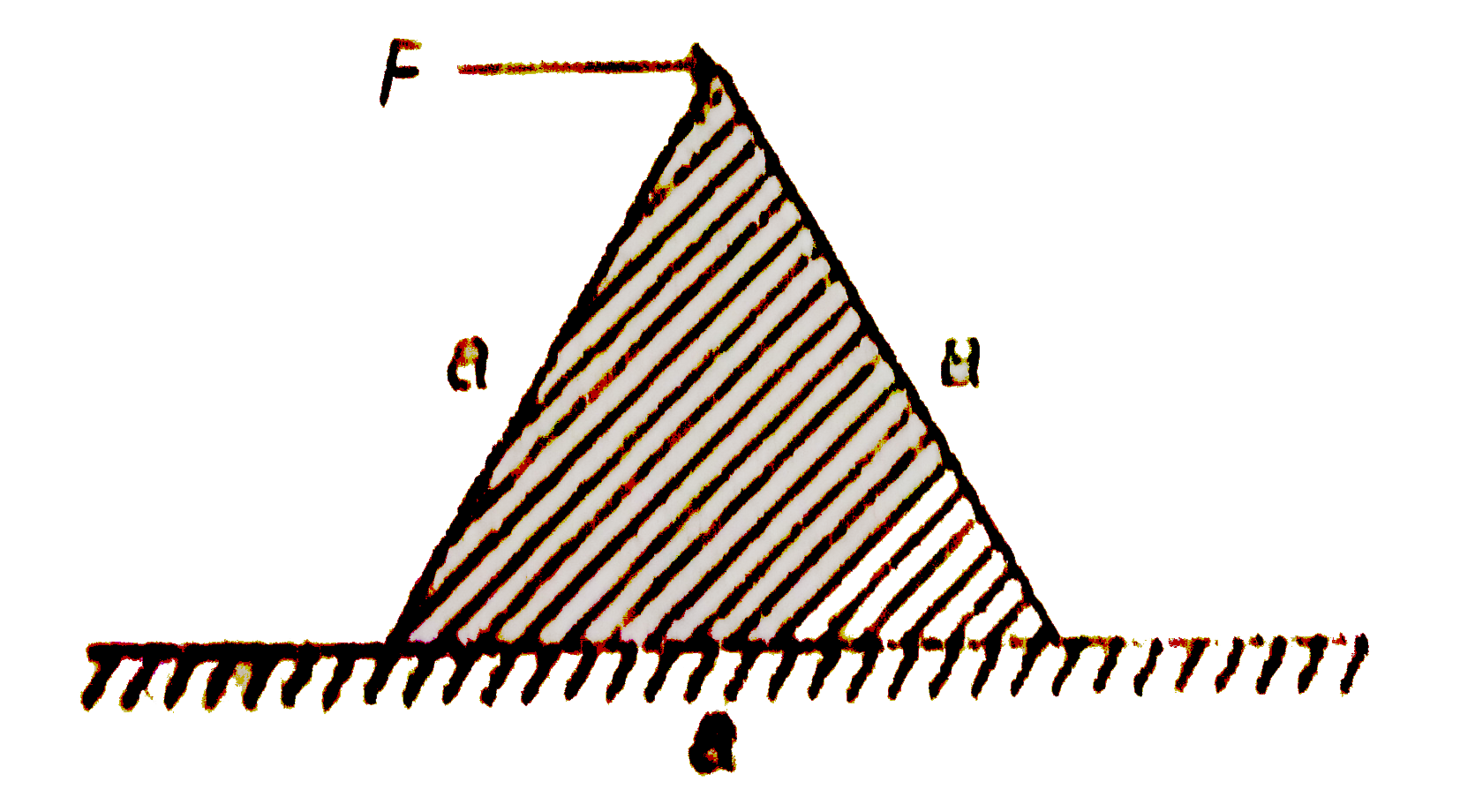
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction mu . A horizontal force F is applied on the top of prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before topping, the minimum force required to topple the prism is
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction mu . A horizontal force F is applied on the prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is
View SolutionA body of mass moving with a velocity in the direction collides with another body of mass moving in direction with a velocity . They coalesce into one body during collision.
View SolutionA body slides down an inclined plane having friction. Indicate the directions of the frictional force and the reaction of the plane on the body.
View SolutionA body of mass m A moving with velocity v collides with another body of mass m 13 moving in the opposite direction with velocity v. After the collision both the bodies get stuck. The velocity of this composite body will be -
View SolutionA body of mass is kept on a rough horizontal surface of friction coefficient . A force is applied horizontally , but the body is not moving .Find the net force exerted by the surface on the body .
View Solution