True or false: a point a b is a critical point of f x y if fx a b and fy a b are undefined.
False. A point is a critical point if both partial derivatives are defined at the point and equal to 0.
Related Solutions
State, true or false:
The point (a,b) lies on the y-axis if b=0.
View SolutionConcavity and convexity :
if then the curve y=f(x) is concave up ( or convex down) in (a,b) and then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point is equal to 0 or undefined)
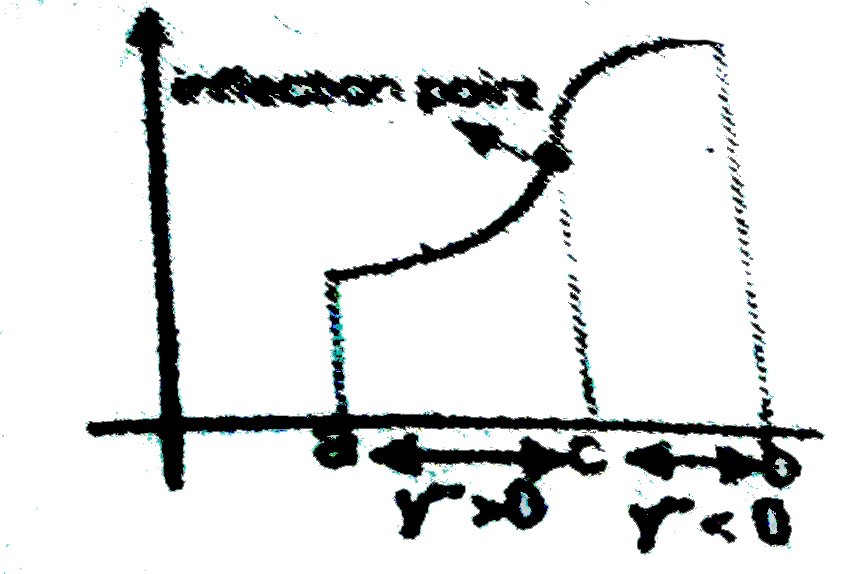
Number of point of inflection for is :
View SolutionConcavity and convexity :
if then the curve y=f(x) is concave up ( or convex down) in (a,b) and then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point is equal to 0 or undefined)
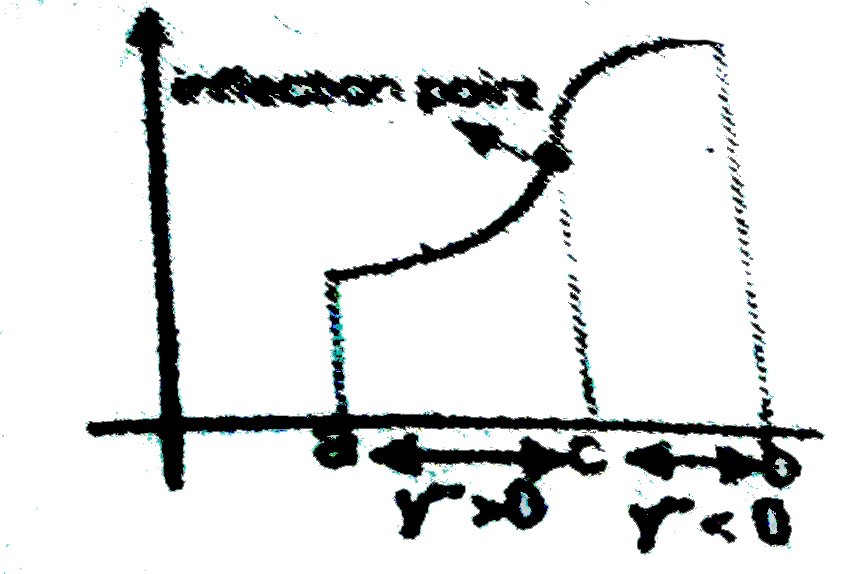
Number of point of inflection for is :
View SolutionWrite True/False:
All critical points of f(x) satisfy f'(x)=0
View SolutionIf is undefined, and , find a and b
View SolutionIf A and B are the points of intersection of y=f(x) and y=f^(-1)(x) , then
View SolutionIf A and B are the points of intersection of y=f(x) and y=f^(-1)(x) , then
View SolutionIf A and B are the points of intersection of y=f(x) and y=f^(-1)(x) , then
View SolutionThe angle between the lines joining the origin to the points of intersection of curve and is
View SolutionIf , then is equal to :
View SolutionIf the point is equidistant from the points and , prove that
View Solutionयदि बिंदु बिन्दुओ P (a ,b ) व Q ( b ,a ) को मिलाने वाले रेखाखण्ड पर स्थित कोई बिंदु है तो सिद्ध कीजिए की
View Solutionयदि विन्दुएं A(a, 0) तथा B(0, b) को मिलानेवाली रेखा P(x, y) को बिन्दु हैं, तो दिखाएँ कि
View SolutionIf the point be equidistant from the points , prove that .
View Solutionयदि बिन्दु P(x, y), बिन्दुओ और से समदूरस्थ है, तो सिद्ध करें कि .
View SolutionIf the point be equidistant from the points , prove that .
View SolutionLet f(x) be a polynomial of degree 3 such that has a critical point at and has a critical point at x = 2. Then f(x) has a local maxima at x = a and local minimum at x = b. Then find b-a.
View SolutionLet f(x) be a polynomial of degree 3 such that has a critical point at and has a critical point at x = 2. Then f(x) has a local maxima at x = a and local minimum at x = b. Then find b-a.
View SolutionTrue or False: underseta oversetbint (f(x))/(f(x)+f(a+b-x))dx=(a+b)/2
View SolutionIf the point is equidistant from the points and , prove that
View Solution