In a metre bridge the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 2 : 3?
Given: l = 100 cm X/R = 2/3
Related Solutions
In a metre bridge, the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 2 : 3?
View SolutionIn a metre bridge, the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 2 : 3?
View SolutionIn a metre bridge the length of the wire is 100 cm. At what point will the balance point be obtained if the two resistances are in the ratio of 4:5 .
View SolutionIn a meter bridge, the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 1:3?
View SolutionIn comparing the resistance of two cells P and Q with a sides wire bridge, a balance point is obtained when the sliding contact is 30 cm from the zero end of the wire. The resistances P and Q are interchanged and the balance is obtained at 120 cm from the same emf. Find the ratio of the resistance P and Q and the length of the bridge wire
View SolutionIn comparing the resistance of two cells P and Q with a sides wire bridge, a balance point is obtained when the sliding contact is 30 cm from the zero end of the wire. The resistances P and Q are interchanged and the balance is obtained at 120 cm from the same emf. Find the ratio of the resistance P and Q and the length of the bridge wire
View SolutionIf 10 is unplugged from a standard resistance box and 33 cm is the balancing length obtained in the metre bridge, then calculate the resistance of the wire.
View SolutionA wire of length 3 m connected in the left gap of a metre bridge balances a resistance in the right gap at a point, which divides the bridge wire in the ratio of . What is the length of the wire corresponding to a resistance of the length of the wire corresponding to a resistance of ?
View SolutionIf the balancing point is obtained at cm on a metre bridge , then the ratio of resistances in the gaps is
View SolutionIf the balance point is obtained at the 35th cm in a metre bridge the resistances in the left and right gaps are in the ratio of
View SolutionThe distance between the positions of two null points obtained in a metre brige wire of length 100 cm , by interchaging a known resistance of and an unknown resistance in the two gaps , is 28.6 cm . Find the value of the unknown resistance .
View SolutionA resistance wire connected in left gap of a metre bridge balances a 10 ohm resistance in right gap at point which divides bridge wire in ratio 3:2. if length of resistance wire is 1.5 m then length of 1 ohm of resistance wire is
View SolutionA resistance wire connected in the left gap of a metre bridge balances a 10Omega resistance in the right gap at a point which divides the bridge wire in the ratio 3:2 . If the length of the resistance wire is 1.5 m, then the length of 1Omega of the resistance wire is:
View SolutionA resistance wire connected in the left gap of a metre bridge balances a 10Ω resistance in the right gap at a point which divides the bridge wire in the ratio 3:2. If the length of the resistance wire is 1.5m, then find the length of 1Ω of the resistance wire.
View SolutionWhy should the balance point be obtained in the middle of the wire of a metre bridge?
View SolutionIn a metre bridge, the gaps are closed by two resistance and and the balance point is obtained at . When is shunted by a resistance of , the balance point shifts to . The values of and are.
 .
.
View SolutionIn a metre bridge expt, when the resistances in the gaps are interchanged the balance point is increases by 10 cm. The ratio of the resistances is
View SolutionTwo resistances 2 ohm and 3 ohm are connected across the two gaps of the metre bridge as shown in the figure .Calculate the current through the cell when the bridge is balanced and the specific resistance of the material of the metre bridge wire. Given the resistance of the bridge wire is 1.49 ohm and its diameter is 0.12 cm.
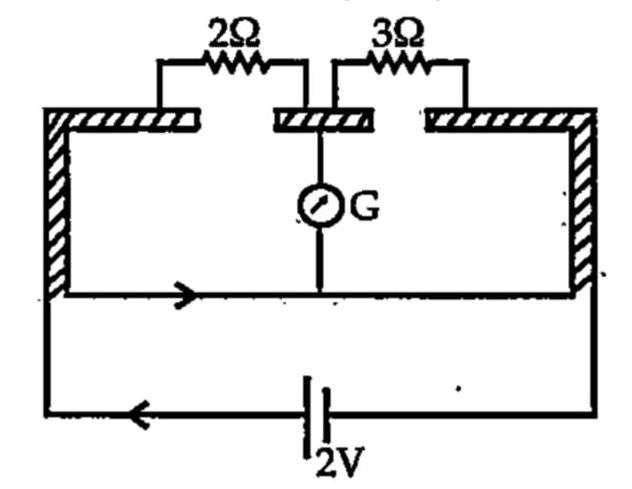
View SolutionTwo resistance 2 ohm and 3 ogm are connected across the two gaps of the metre bridge as shown in figure. Calculate the current through the cell when the bridge is balanced and the specific resistance of the material of the metre bridge wire. Given the resistance of the bridge wire is 1.49 ohm and its diameter is 0.12 cm.
View Solutionएक तार मीटर ब्रिज के बायें अन्तराल में जोड़ा जाता है, जो दाएँ अन्तराल में के प्रतिरोध को उस बिन्दु तक संतुलित करता है जो ब्रिज के तार को 3 : 2 के अनुपात में विभाजित करता हो। यदि तार की लम्बाई 1 m हो तब एक ओम के तार की लम्बाई होगी
View Solution