Derive an expression for the electrostatic energy of a spherical nucleus of radius R assuming that the charge q = Ze is uniformly distributed homogeneously in the nuclear volume.
The charge density ρ = 3ze/4π R3. Consider a spherical shell of radii r and r + dr. The volume of the shell is 4πr2dr. The charge in the shell q = 4πr2drρ. The electrostatic energy due to the charge q and the charge q of the sphere of radius r which is 4/3πr3ρ is calculated by imagining q to be deposited at the centre. The charge outside the sphere of radius r does not contribute to this energy Fig. 8.8. ThusThe total electrostatic energy is obtained by integrating the above expression in the limits 0 to R
Related Solutions
A charge Q coulomb is uniformly distributed over a sphere volume of radius R metres. What will be the expression for the energy of the system.
View SolutionA charge Q coulomb is uniformly distributed over a sphere volume of radius R metres. Obtain an expression for the energy of the system.
View SolutionA charge is uniformly distributed in a spherical volume of radius R. A particle of charge and mass m is projected with velocity from the surface of the spherical volume to its centre. The minimum value of such that it just reaches the centre (assume that there is no resistance on the particle except electrostatic force) of the spherical volume is
View Solutionelectrostatic energy of a nucleus of a Ze charge kZ^(2)e^(2)//R where k is a constant and R is the nuclear radius. This nucleus splits into two daughter nuclei having Ze/2 charge. If these two daughter nuclei move far away from each other, then what will be the value of the change in electrostatic energy in this process?
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre is
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionFind out energy stored inside a solid non-conducting sphere of total charge Q and radius R. [Assume charge is uniformly distributed in its volume.]
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View SolutionFind the electrostatic potential energy of the following charge configuration. A non conducting thin spherical shell of radius R with a total charge Q spread on it uniformly.
View SolutionQ charge is distributed uniformly through the volume of a sphere of radius R, The energy of the system will be—
View Solutionनाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
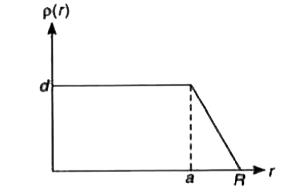
दूरी r= R पर वैघुत क्षेत्र है।
View SolutionR त्रिज्या का पतला गोलीय कोश समान रूप से आवेशित है , जिस पर आवेश Q है। गोली कोश के केंद्र से r दुरी पर स्थिरवैद्युत विभव का मान होगा।
View Solutionत्रिज्या R के एक नाभिक में नाभिकीय आवेश (Ze) असमान रूप से वितरित है चित्रानुसार, आवेश घनत्व [प्रति इकाई आयतन आवेश] नाभिक के केंद्र से त्रिज्यीय दूरी r पर निर्भर करता है विधुत क्षेत्र केवल त्रिज्यीय दिशा के अनुदिश है।
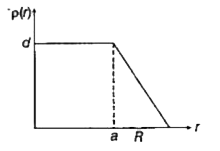
नाभिक के अन्दर यह देखा गया है विधुत क्षेत्र सामान्यतः रेखिक रूप से r पर निर्भर करता है यह व्यक्त करता है।
View Solution(i). A charge of Q coulomb is uniformly distributed over a spherical volume of radius R metre Obtain an expression for the energy of the system.
(ii). What will be the corresponding expression for the energy needed to completely diassemble the planet earth against the gravitational pull amongst its constituent particles? Assume the earth to be a sphere of uniform mass density. calculate the energy, given that the product of the mass and the radius of the earth to be
View Solutionr त्रिज्या वाले एक गोलीय चालक के पृष्ठ पर q आवेश एकसमान रूप से वितरित है।
गोल के अंदर विद्युत क्षेत्र क्या होगा
View Solutionनाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
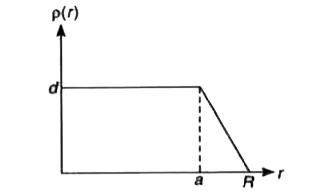
a= 0 के लिए d (p का अधिकतम मान) का मान है।
View SolutionIf a thin spherical shell of radius r and charge q is kept inside a thick spherical shell of inner radius 2r, outer radius 3r, and total charge 2q. (a) Find the charge distribution on each surface. (b) Find the self-energy of each charge distribution. (c) Find the total electrostatic energy stored in the system.
View SolutionFind out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View Solution