A particle of mass M is elastically scattered through an angle θ from a target particle of mass m initially at rest M > m. a Show that the largest possible scattering angle θmax in the Lab. System is given by sin θmax = m/M the corresponding angle in the CMS being cosθ∗max = −m/M. b Further show that the maximum recoil angle for m is given by sinϕmax = [M −m/2M]1/2. c Calculate the angle θmax + ϕmax for elastic collisions between the incident deuterons and target protons.
a We can work out this problem in the LS but we prefer the CMS for convenience. Writing the equation for transformation of angles
Related Solutions
A particle of mass m having collided a stationary particle of mass M deviated by an angle whereas the particle M recoiled at an angle to the direction of the initial motion of the particle m. How much in percent and in what way has the kinetic energy of this system changed after the collision, if M/m = 5 ?
View SolutionA particle of mass m having collides with a stationary particle of mass M deviated by an angle whereas the particle M recoiled at an angle to the direction of theinitial motion of the particle m. How much in percent and in what way has the kinetic energy of this system changed after the collision, if .
View SolutionA ball of mass M collides elastically with another stationary ball of mass m. If , find the maximum angle of deflection of M.
View SolutionA particle of mass m collides with a stationary particle of mass M and deviates by an angle of 60°. After collision mass M recoils at an angle 30° to the original direction of motion of m. If there is no loss in kinetic energy in the collision, the ratio of m/M is _________.
View SolutionIf , then .
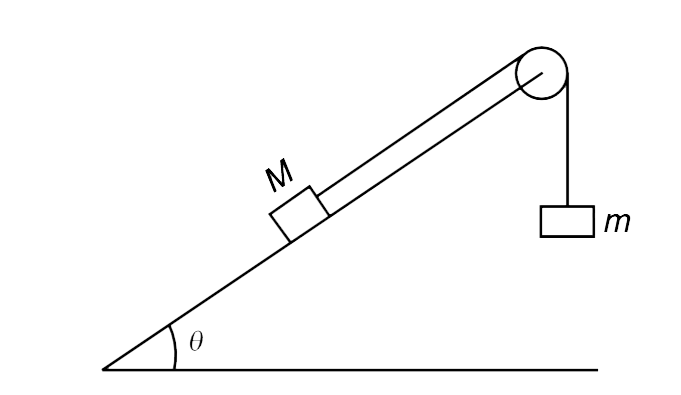
View SolutionA particle of mass M rests on a rough inclined plane at an angle q to the horizontal. It is connected to another mass m as shown in fig. The pulley and string are light. The largest value of m for which equilibrium is possible is M. Find the smallest value of m for which equilibrium is possible
View SolutionIn ABC, m A = m B = , m C = . Is this triangle possible ? Why?
View SolutionA sphere of mass m , impinges obliquely on a sphere, of mass M, which is at rest. Show that, if m=eM , the directions of motion of the sphere after impact are at right angles.
View SolutionA sphere of mass m , impinges obliquely on a sphere, of mass M, which is at rest. Show that, if m=eM , the directions of motion of the sphere after impact are at right angles.
View SolutionIn the given figure, m(arc AYB) = m(are PXQ), then m angle POQ =______
View SolutionABCD ବୃତ୍ତାନ୍ତର୍ଲିଖିତ ଚତୁର୍ଭୁଜର |, ହେଲେ ଓ ର ଅନ୍ତର କେତେ ହେବ ?
View SolutionIn the given figures, if m angle PAB = 50^@ , m angle PQB =
View SolutionA system consists of two particles of masses M and m(M>m) separated by distanced.What will be the position of CM?
View SolutionFigure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
View SolutionA partical of mass moving with velocity collides perfectly elastically with another particle of mass . If the incident particle is deflected by . The heavy mass will make and angle with the initial direction of equal to:
View SolutionA particle of mass m has a velocity of 1 m s^(-1) , which makes a perfectly elastic collision with another stationary particle of mass 2 m. If, the incident particle 90^@ is deflected by. A heavy mass m makes an angle A with the initial direction, that is equal to:
View Solutiontriangle ABC ଓ triangle DEF ମଧ୍ୟରେ m angle A = m angle D, m angle B = m angle E, AB = 3 ସେ.ମି., BC = 5 ସେ.ମି. ଏବଂ DE = 7.5 ସେ.ମି. ହେଲେ EF = __ସେ.ମି. ?
View SolutionA particle of mass m having collided with a stationary particle of mass M deviated by an angle whereas the particle M recoiled at an angle to the direction of the initial motion of the particle m. How much (in per cent) and in what way has the kinetic energy of this system changed after the collision, if ?
View Solutionଦତ୍ତ ଚିତ୍ରରେ, ଓ ~ ହେଲେ କେତେ ହେବ ?
View SolutionAn object of mass M V_(0) It collides with an effortless mass 'm' at speed. After the collision both the masses move from the initial direction of M. theta_(1) And thta_(2) moves at angles. The maximum value of the ratio M/m, for which the angle theta_(1) And theta_(2) will be equal to :
View Solution