In an apparatus constructed by Academician Rebinder the value of the surface tension is determined from the difference in pressure ΔP required to produce an air bubble at the end of a capillary tube of radius r immersed in the liquid under investigation Fig.. Calculate the surface tension if r equals 1 mm and ΔP equals 14 mm of water. The end of the capillary tube is near the surface of the liquid.
Answer:Explanation:The magnitude of the additional pressure arising in the air bubble inside the liquid as a result of the action of the forces of surface tension may be determined from the following considerations.When the end of the capillary tube comes in contact with the surface of the liquid the liquid rises in the capillary to a height h = lα/dgr under the action of the surface force F = 2πrα directed upwards. The force F is then balanced by the weight of the liquid column.If an additional pressure is created in the capillary tube over the surface of the liquid of magnitudeS = πr2 is the area of the capillary cross-section then the action of the surface tension forces will be equalized by the force of the excess pressure of the air in the capillary and the weight of the liquid column in the capillary tube will be unbalanced. Therefore the level of the liquid in the capillary should drop to the initial height and an air bubble will form at the end of the tube i.e. a hemisphere of radius R equal to the radius of the capillary tube r. The pressure inside the bubble will bewhere R is the radius of the bubble.It may be shown that this expression always determines the excess pressure resulting from the surface tension in closed bubbles in liquids.From expression 1 it is seen that the pressure in the bubble decreases with an increase in the radius of the bubble. From a direct examination of the process of bubble formation at the end of the capillary tube it follows that the smallest value of the radius of the bubble is equal to the radius of the capillary tube.Consequently in calculating a from the data in the example it is necessary to substitute into the formula
Related Solutions
In a device designed by Academician Rebinder the surface tension is determnined from the pressure difference required to form a bubble of air at the end of a capillary immersed in the liquid being investigated (fig). Calculated the surface tension if the radius of the capillary is r = 1 mm and the difference in the pressures during bubble formation is DeltaP = 14 mm of water column. The end of the capillary is near the surface of the liquid.
View SolutionIn a device designed by Academician Rebinder the surface tension is determnined from the pressure difference required to form a bubble of air at the end of a capillary immersed in the liquid being investigated (fig). Calculated the surface tension if the radius of the capillary is and the difference in the pressures during bubble formation is of water column. The end of the capillary is near the surface of the liquid.
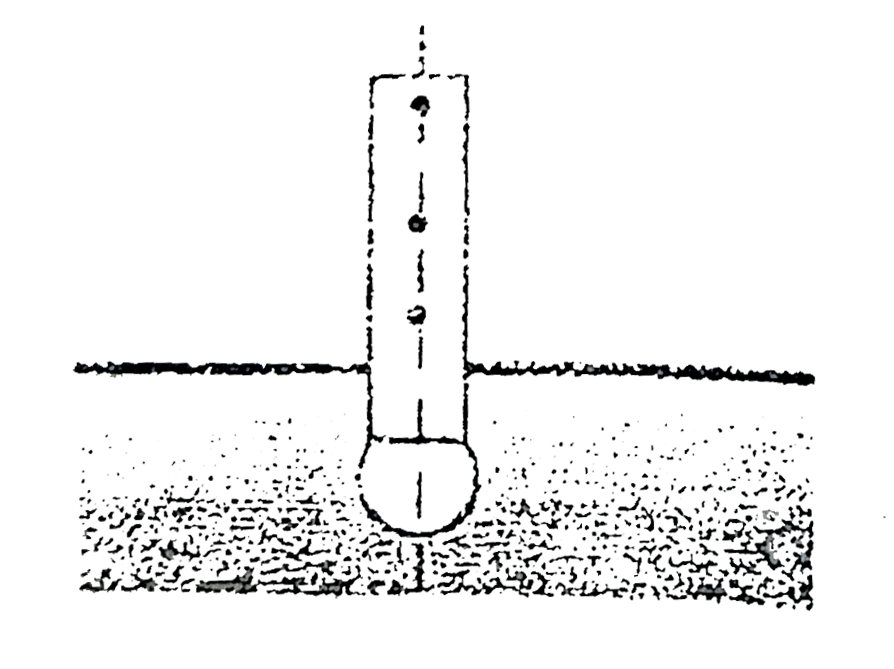
View SolutionThe weight of liquid column in a capillary tube is 11xx10^(-1)N . If the radius of tube is 7 mm, calculate the surface tension of liquid.
View SolutionThe weight of liquid column in a capillary tube is 11xx10^(-4)N . If the radius of tube is 7 mm, calculate the surface tension of liquid.
View SolutionThe weight of liquid column in a capillary tube is 11xx10^(-4)N . If the radius of tube is 7 mm, calculate the surface tension of liquid.
View Solutionमिमी व्यास के निम्नतम सिरे वाली केशनली को बीकर में उपस्थित जल की सतह से सेमी निचे डुबोया जाता है। जल में केशनली के अंत में अर्द्धगोलीय बुलबुला बनाने हेतु आवश्यक दाब का मान होगा
View SolutionA capilary tube is kept vertical and made to touch the surface of the liquid of surface tension T . If the radius of the capillary tube is 'r' . Then the force on the wall of the capillary tube is
View SolutionGive the expression for surface tension of a liquid in a capillary tube.
View SolutionIn a capillary tube, the liquid rises to a height of 8cm and surface tension of liquid is 70 dyne/cm. Then the radius of capillary tube is
View SolutionA narrow capillary tube is dipped below water surface and a liquid bubble of radius formed at the lower end by blowing air through the tube.
a. Calculate the excess pressure due to surface tension.
b. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water?
The surface tension of water at temperature of the experiment is . 1 atmospheric pressure , density of water
View SolutionA narrow capillary tube is dipped 10 cm below water surface and a liquid bubble of radius 2 mm formed at the lower end by blowing air through the tube. a. Calculate the excess pressure due to surface tension. b. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiment is 7.30xx10^(-2) N//m . 1 atmospheric pressure = 10^(5) Pa , density of water = 1000 kg//m^(3)
View SolutionThe surface tension of water is . If 1 mm be the radius of a capillary tube then what will be the capillary Rise?
View SolutionA glass capillary tube of internal radius is immersed in water. The top end of the tube projects by above the surface of water. At what angle does the liquid meet the tube? Surface tension of water .
View SolutionA glass capillary tube of internal radius r=0.25 mm is immersed in water. The top end of the tube projects by 2 cm above the surface of water. At what angle does the liquid meet the tube? Surface tension of water =0.7Nm^(-1) .
View SolutionCalculate the difference in water levels in two commnicating capillary tube of radius and . Surface tension of water

View SolutionCalculate the difference in water levels in two commnicating capillary tube of radius and . Surface tension of water

View SolutionA glass capillary tube of internal radius is immersed in water. The top end of the tube projects by above the surface of water. At what angle does the liquid meet the tube? Surface tension of water .
View SolutionA capillary tube of radius r is dipped vertically in a liquid of density d, surface tension T and angle of contact theta then the pressure difference just below the two surface, one in the beaker and the other in the capillary tube, is :
View SolutionA capillary tube of radius r is dipped vertically in a liquid of density d, surface tension T and angle of contact then the pressure difference just below the two surface, one in the beaker and the other in the capillary tube, is :
View Solution