What are the three different ways of representing a polynomial using arrays? Represent the following polynomials using any three different methods and compare their advantages and disadvantages. i 7x5 - 8x4 + 5x3 + x2 + 2x + 15 ii 3x100 5x55 - 10
A general polynomial Ax can be written as an Xn + an- 1 X n-1 + ...+a1x+a0 where an ≠0 then we can represent Ax 1. As an ordered list of coefficients using a one dimensional array of length n+2 A=n an an-1 … a1 a0 the first element is the degree of A followed by n+1 coefficients in order of decreasing exponent. So the given polynomial can be represented asi. 5 7 -8 5 1 2 15ii. 100 3 0 0 0 0…45 times -5 0 0 0…55 times -10 Advantage of this method is simple algorithms for addition and multiplication as we have avoided the need to explicitly store the exponent of each term. However there is a major disadvantage of this method and that is wastage of memory for certain polynomial like example ii because we are storing more zero values than non-zero values. 2. As an ordered list where we keep only non-zero coefficient along with their exponent like m em-1 bm-1 em-2 bm-2 … e0 b0 where first entry is the number of nonzero terms then for each term there are two entries representing an exponentcoefficient pair. So the given polynomial can be represented as i. 6 5 7 4 -8 3 5 2 1 1 2 0 15ii. 3 100 3 55 -5 0 -10This method is solves our problem of wasted memory like what happened in example 2.
Related Solutions
निम्नलिखित बिन्दियों का प्रयोग करते हुए 15 को प्रदर्शित करने वाले संयोजित (array) आरेख हैं

15 अथवा अन्य किसी संख्या को प्रदर्शित करने के उपरोक्त तरीके को ...... की संकल्पना पढ़ाने के लिए इस्तेमाल किया जा सकता है।
View Solutionनिम्नलिखित बिंदियों का प्रयोग करते हुए 15 को प्रदर्शित करने वाले संयोजित (array) आरेख हैं-
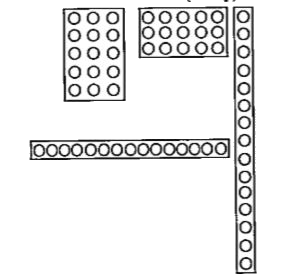
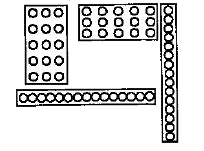
15 अथवा अन्य किसी संख्या को प्रदर्शित करने के उपर्युक्त तरीके को ______ की संकल्पना पढ़ाने के लिए इस्तेमाल किया जा सकता है।
View SolutionFollowing are array diagrams using bindis to represent 15.

The way of representing 15 or any other number in the above manner can be used to teach concept of
View SolutionFollowing are array diagram using bindis to represent 15.
The way of representing 15 or any other number in the above manner can be used to teach concept of
View SolutionState any three advantages and disadvantages of friction.
View Solutionమూడు వేర్వేరు బాహుపదులను వ్రాసి, ప్రతి దానికి మూడు ప్రశ్నల చొప్పున రూపొందించండి.
View SolutionWhat are the advantages and disadvantages of using charcoal as a fuel as compared to wood ?
View SolutionWhat are the advantages and disadvantages of using charcoal as a fuel as compared to wood ?
View Solutionসমক পার্থক্যের সংজ্ঞা দাও। বিস্তৃতির পরিমাপক হিসেবে এর ব্যবহারের সুবিধা ও অসুবিধা আলােচনা করো।
View Solutionചുവടെപ്പറയുന്ന തരത്തിലുള്ള p(x) എന്ന ബഹുപദങ്ങള് കണ്ടുപിടിക്കുക.
p(0)=0, p(1) = 2 ആയ മൂന്നു വ്യത്യസ്ത രണ്ടാംകൃതി ബഹുപദങ്ങള്
View SolutionWhat are the advantages and disadvantages of using fertilizers?
View SolutionWhat are the advantages and disadvantages in using a vice?
View SolutionDifferent methods are used to purify organic compounds. Name any three methods of purification.
View SolutionWrite three advantages & disadvantages of GMO.
View SolutionWhich of the following statements is true regarding Numeral' and 'Number'?
(I) A numeral is a symbol used to represent number.
(II) Same number can be represented by different nnumerals.
View SolutionWhat are the three different types of iron? Write their uses.
View SolutionA company is manufacturing televisions, refrigerators, air conditioners, washing machines and stoves using different productive resources. Suggest a suitable organisational structure for the company and explain any three advantages and disadvantages, each of this structure.
View Solutionరెండు శూన్యలు కలిగిన ఏవేని మూడు బహుపదులను వ్రాయండి.
View SolutionExplain any three features of underground mining method used in different countries of the world.
View SolutionWhat are the advantages and disadvantages of using a reflecting telescope?
View Solution