Derive the formula for the velocity distribution of gas molecules of mass m at Kelvin temperature T.
Consider a two-body collision between two similar gas molecules of initial velocity ν1 and ν2. After the collision let the final velocities be ν3 and ν4. The probability for the occurrence of such a collision will be proportional to the number of molecules per unit volume having these velocities that is to the product f ν1 f ν2. Thus the number of each collisions per unit volume per unit time is c f ν1 f ν2 where c is a constant. Similarly the number of inverse collisions per unit volume per unit time is c f ν3 f ν4 where c is also a constant. Since the gas is in equilibrium and the velocity distribution is unchanged by collisions these two rates must be equal. Further in the centre of mass these two collisions appear to be equivalent so that c = c. We can then writewhere A and α are constants. The negative sign is essential to ensure that no molecule can have infinite energy. Let Nνdν be the number of molecules per unit volume with speeds ν to +dν irrespective of direction. As the velocity distribution is assumed to be spherically symmetrical Nνdν is equal to the number of velocity vectors whose tips end up in the volume of the shell defined by the radii ν and +dν so thatwhere gamma functions have been used for the evaluation of the two integrals. Further
Related Solutions
ताप T पर M अणु भार वाली गैस के अणुओं का औसत वेग है-
View SolutionThe average velocity of molecules of a gas of molecilar weight (M) at temperature (T) is
View SolutionThe average velocity of molecules of a gas of molecular weight (M) at temperature (T) is
View SolutionIf the thermal energy of a monoatomic gas molecules of mass m at temperature T kelvin is of the order of , then the deBroglie wavelength of the matter waves is of the order of
View SolutionA gas is equilibrium at T kelvin. If mass of one molecule is m and its component of velocity in x direction is vx. Then mean of its v_(x)^(2) is-
View SolutionThe rms velocity of a gas molecule of mass m at a given temperature is proportional to
View SolutionThe root mean square velocity of a gas molecule at any temperature T K of a gas molecule of molecular weight M is
View SolutionA gas consists of molecules of mass m and is at a temperature T . Making use of the Maxwell velocity distribution function, find the corresponding distribution of the molecules over the kinetic energies epsilon . Determine the most probable value of a gas the kinetic energy epsilon_p . Does epsilon_p correspond to the most probable velocity ?
View SolutionAt certain temperature, the r.m.s. velocity for CH_4 gas molecules is 100 m/sec. This velocity for SO_2 gas molecules at same temperature will be
View SolutionAt certain temperature, the r.m.s. velocity for gas molecules is 100 m/sec. This velocity for gas molecules at same temperature will be
View SolutionIf m represents the mass of each molecule of a gas and T, its absolute temperature, then the root mean square velocity of the gaseous molecule is proportional to
View SolutionRead the following paragraph and answer the questions given below: According to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to ump (most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature. In general, the distribution depends upon the value of (M)/(T) (where M is molar mass and T is temperature in kelvin). Choose the correct option: On increasing temperature, which of the following statement is incorrect?
View SolutionN molecules each of mass m of gas A and 2N molecules each of mass 2m of gas B are contained in the same vessel at temperature T. The mean square of the velocity of molecules of gas B is and the mean square of x component of the velocity of molecules of gas A is . The ratio is
View SolutionN molecules each of mass m of gas A and 2N molecules each of mass 2m of gas B are contained in the same vessel at temperature T. The mean square of the velocity of molecules of gas B is and the mean square of x component of the velocity of molecules of gas A is . The ratio is
View SolutionAccording to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to .(most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature. In general, the distribution depends upon the value of (where M is molar mass and Tis temperature in kelvin).
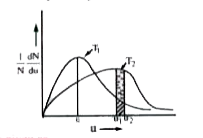
On increasing the temperature, number of molecules having speed between
View SolutionRead the following paragraph and answer the questions given below:
According to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to ump (most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature.
In general, the distribution depends upon the value of (where M is molar mass and T is temperature in kelvin).
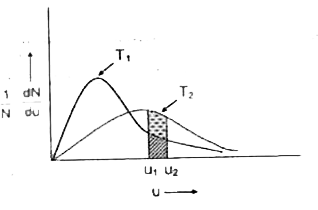
Choose the correct option:
Relationship between a is given as
View SolutionFrom the Maxwell distribution function frind , the mean value of the squared projection of the molecular velocity in a gas at a temperature . The mass of each molecule is equal to .
View SolutionUsing the Maxwell distribution function, calculate the mean velocity projection and the mean value of the modules of this projection if the mass of each molecule is equal to and the gas temperature is .
View Solutionगैस के अणुओं का औसत वेग 400 मी /से है। समान ताप पर गैस के अणुओं के वर्ग - माध्य मूल वेग (rms velocity) की गणना कीजिए।
View SolutionMaking use of the Maxwell distribution function, calculate the number of gas molecules reaching a unit area of a wall per unit time, if the concentration of molecules is equal to , the temperature to , and the mass of each molecule is .
View Solution