a Sketch the one-dimensional “top hat” potential 1 V = 0 for x L. b Consider particles of mass m and energy E < W incident on this potential barrier from the left x < 0. Including possible reflections from the barrier boundaries write down general expressions for the wavefunctions in these regions and the form the time-independent Schrodinger equation takes in each region. What ratio of wavefunction amplitudes is needed to determine the transmission coefficient? c Write down the boundary conditions for ψ and dψ/dx at x = 0 and x = L. d A full algebraic solution for these boundary conditions is time consuming. In the approximation for a tall or wide barrier the transmission coefficient T is given byDetermine T for electrons of energy E = 2eV striking a potential of value W = 5eV and width L = 0.3nm. e Describe four examples where quantum mechanical tunneling is observed.
The second term is absent as there is no reflected wave coming from right to lefte Examples of quantum mechanical tunneling i α-decay Observed α-energy may be ∼ 5 MeV although the Coulomb barrier height is 20 or 30 MeV ii Tunnel diode iii Josephson effect In superconductivity electron emission in pairs through insulator is possible via tunneling mechanism iv Inversion spectral line in ammonia molecule. This arises due to tunneling through the potential barrier between two equilibrium positions of the nitrogen atom along the axis of the pyramid molecule which is perpendicular to the plane of the hydrogen atoms. The oscillation between the two equilibrium positions causes an intense spectral line in the microwave region.
Related Solutions
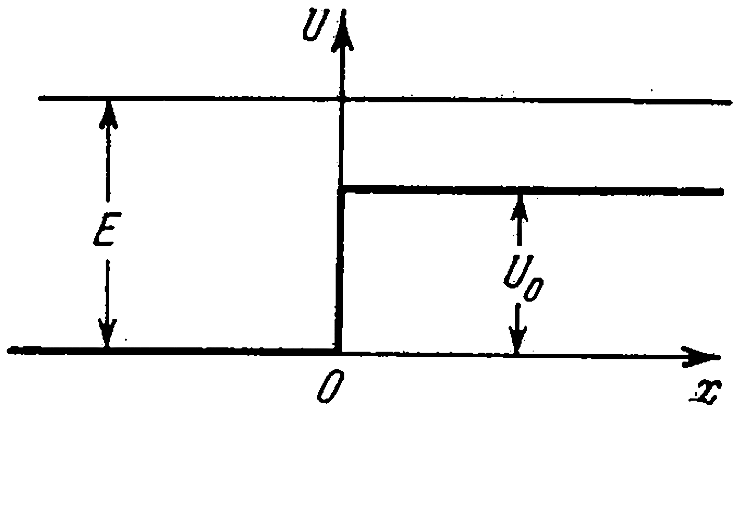
Particle of mass and energy moves from the left to the potential barrier shown in figure. Find:
(a) the reflection coefficient of the barrier for
(b) the effective penetration depth of the particles into the region for i.e., the distacne from the barrier boundary to the point at which the probability of finding a particle decreases e-fold
View SolutionThe wavefunction of a particle of mass in a unidimensional potential field has in the ground state the form , where is a normalization factor and is positive constant. Making use of a Schrodinger equation, find the constant and the energy of the particle in this state.
View SolutionConsider a one -dimensional motion of a particle with total energy E. There are four regions A,B,C and D in which the relation between potential energy E. There are four regions A,B,C and D in which the relation between potential energy V, kinetic energy (K) and total energy E is as given below Region A : V gt E Region B: V lt E Region C :K gt E Region D : V gt E . State with reasons in each
View SolutionUsing Eq.(6.2e), find the probability of a particle of mass and energy tunneling through the potential barrier shown in fig. where .
View SolutionIn a forward biased - junction diode, the potential barrier in the depletion region is of the from...
View SolutionIn a forward biased - junction diode, the potential barrier in the depletion region is of the from...
View SolutionIn a forward biased - junction diode, the potential barrier in the depletion region is of the from...
View SolutionThe gravitational field in a region is given by E = (5hat(i) + 12 hat(j)) Nkg^(-1) . If a particle of mass 2kg is moved from the origin to the point (12 m, 15 m) in this region, the change in gravitational potential energy is
View SolutionA potential barrier of 0.3 V exists across a p-n junction. If the depletion region is 1 m wide, what is the intensity of electric field in this region?
View SolutionA potential barrier of 0.3 V exists across a p-n junction. If the depletion region is 1 mu m wide, what is the intensity of electric field in this region?
View SolutionIn a forward biased p-njunction diode, the potential barrier in the depletion region is of the form
View SolutionWhat do you mean by barrier potential and depletion region of a pn junction?
View SolutionA particle with total energy E moves in one dimensional region where the potential energy is U(x) The speed of the particle is zero where
View SolutionAn electron with energy E is incident on a potential energy barrier of height and thickness L. The probability of tunneling increases if
View SolutionIn a p-n junction, the thickness of depletion region is and potential barrier across the junction is 0.20 V
What will be the intensity of electric field in this region ?
View SolutionA potential barrier of 0.6 V exists across a P - N junction . If the depletion region is 1mu m wide, what is the intensity of electric field in the region?
View SolutionA particle with total energy E is moving in a potential energy region U (x). Motion of the particle is restricted to the region when
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionA particle with total energy E is moving in a potential energy region U(x).Motion of the particle is restricted to the region when
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View Solution