The figure shows a radiant energy spectrum graph for a black body at a temperature T. Choose the correct statementsA The radiant energy is not equally distributed among all the possible wavelengths B For a particular wavelength the spectral intensity is maximum C The area under the curve is equal to the total rate at which heat is radiated by the body at that temperature D None of these
Correct option A B Explanation:Area under the curve gives the rate at which heat per unit surface is radiated by the body. i.e. total rate of heat radiation = Area under the curve × Surface area of the body.
Related Solutions
The shows a radiant energy spectrum graph for a black body at at temperature
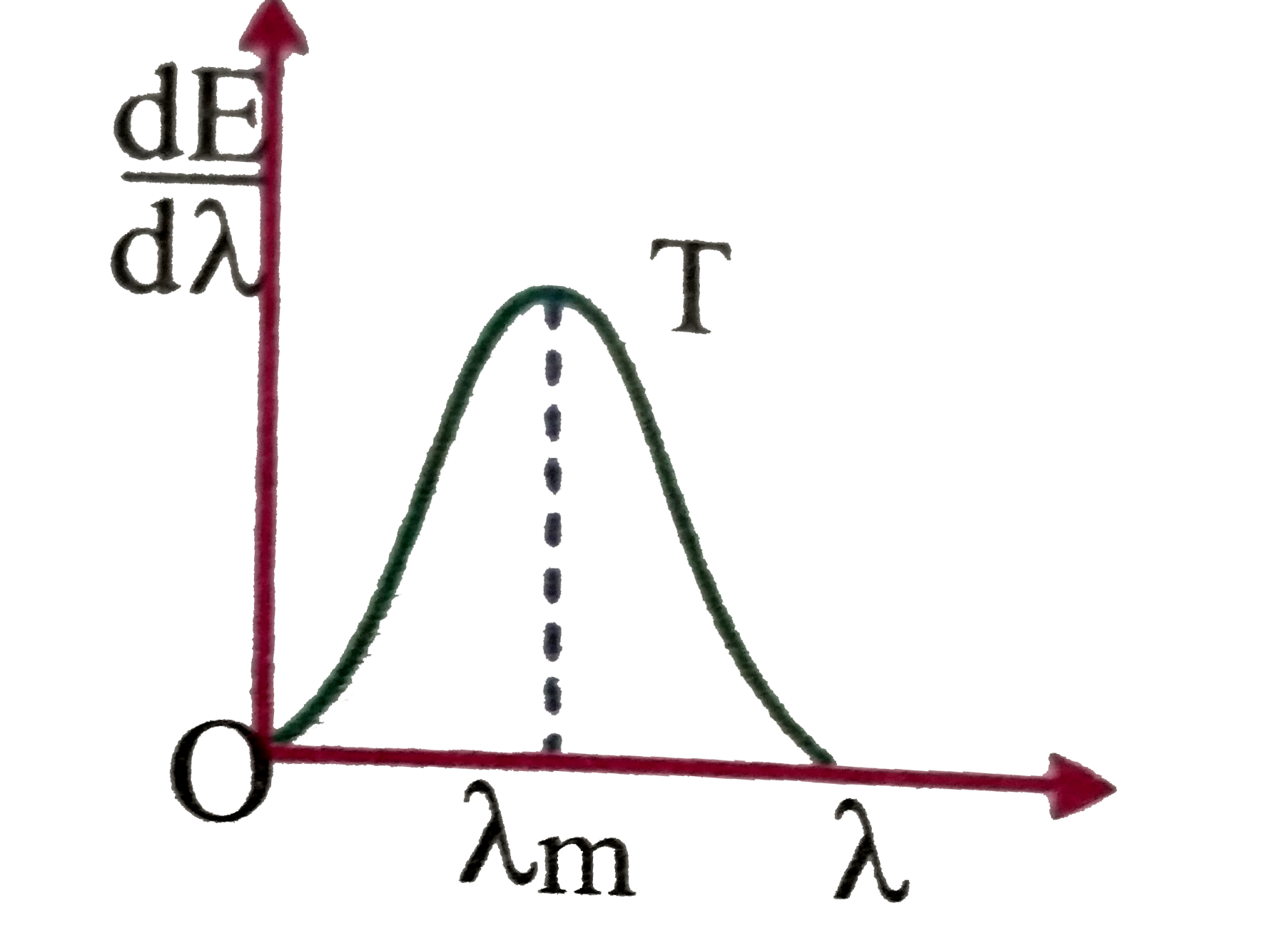
If the temperature of the body is raised to a higher temperature then choose the correct statement (s).
View SolutionThe shows a radiant energy spectrum graph for a black body at at temperature
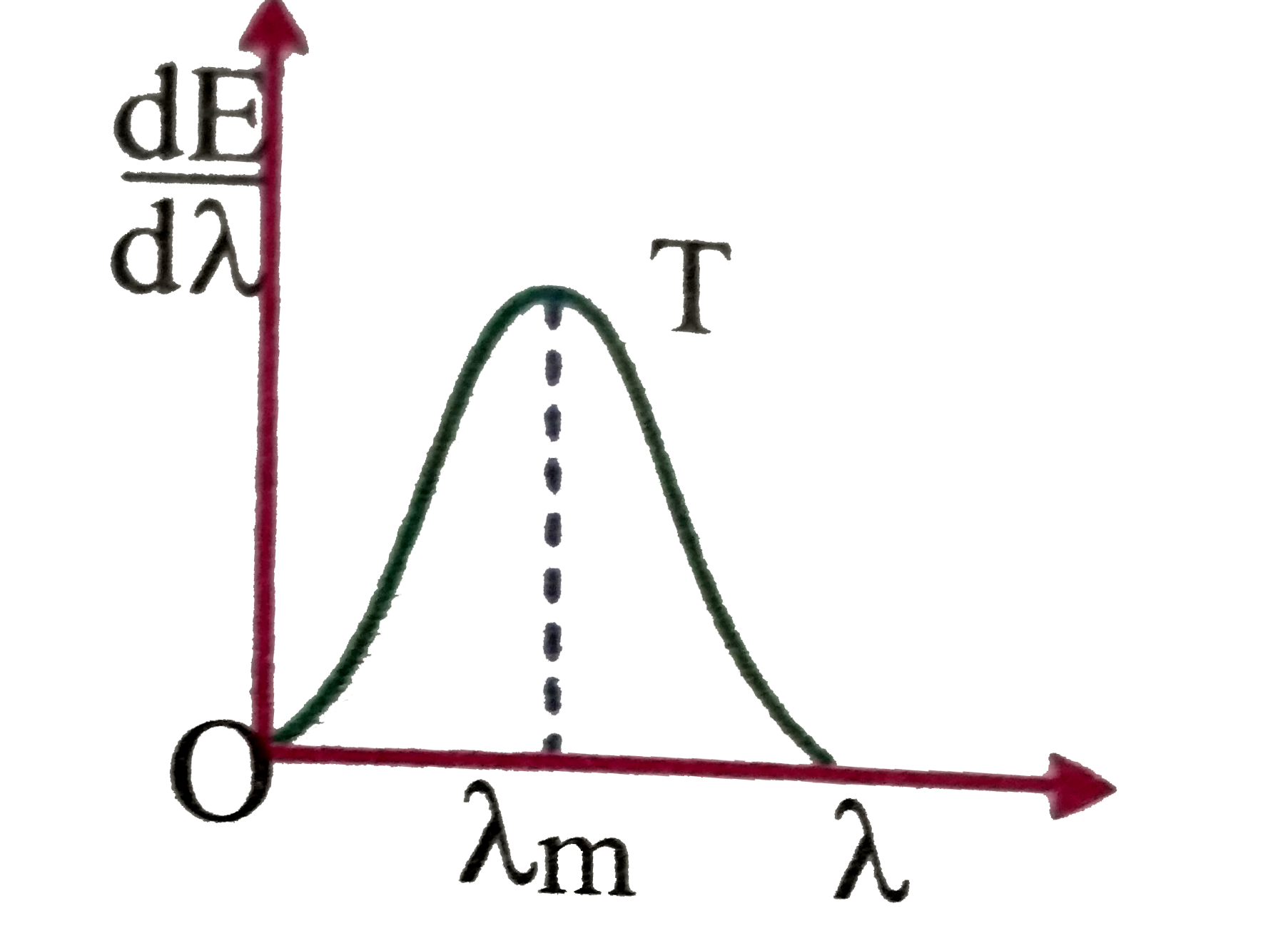
Choose the correct statements (s) .
View SolutionTwo bodies A and B have emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are the same. The two bodies radiate energy at the same rate. The wavelength l, corresponding to the maximum spectral radiant power in the radiation from B, is shifted from the wavelength corresponding to the maximum spectral radiant power in the radiation from A by m. If the temperature of A is 5802 K.
Find the wavelength of the radiation emitted from body B corresponding to maximum spectral radiant power.
View SolutionA black body radiates energy at the rate of E at a high temperature TK . When the temperature is reduced to , the radiant energy will b
View SolutionA black body radiates energy at the rate of E at a high temperature TK . When the temperature is reduced to , the radiant energy will b
View SolutionThe energy distribution E with the wavelength (lambda) for the black body radiation at temperature Kelvin T is shown in the figure. As the temperature is increased the maxima will
View SolutionA black body radiates energy at the rate of E "watt"//m^(2) at a high temperature TK when the temperature is reduced to [(T)/(2)]K Then radiant energy is .
View SolutionTwo bodies A and B have emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are the same. The two bodies radiate energy at the same rate. The wavelength l, corresponding to the maximum spectral radiant power in the radiation from B, is shifted from the wavelength corresponding to the maximum spectral radiant power in the radiation from A by 10^(-6) m. If the temperature of A is 5802 K. Find the temperature of body B
View SolutionThe original temperature of a black body is . . The temperature at which this black body must be raised so as to double the total radiant energy, is
View SolutionThe wavelength corresponding to maximum spectral radiancy of a black body A is lambda_(A) =5000A .Consider another black body B whose surface area is twice that of A and total radiant energy by B is 16 times that emitted by A .The wavelength corresponding to maximum spectrum radiancy for B will be
View SolutionState Stefan's law. Sketch graphs showing the distribution of energy in the spectrum of black body radiation at three temperatures, and indicate which curve corresponds to the highest temperature.
View SolutionThe energy spectrum of a black body exhibits a maximum around a wavelength . The temperature of the black body is now changed such that the energy is maximum around a wavelength . The power radiated by the black body will now increase by a factor of
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
View SolutionA black body radiates energy at the rate of EW//m^(2) at a high temperature TK. When the temperature is reduces to half, the radiant energy will be
View SolutionStatement I: As the temperature of the black body increases, the wavelength at which the spectral intensity is maximum decreases.
Statement II: The wavelength at which the spectral intensity will be maximum for a black body is proportional to the fourth power of its absolute temperature.
View SolutionStatement I: As the temperature of the black body increases, the wavelength at which the spectral intensity (E_lamda) is maximum decreases. Statement II: The wavelength at which the spectral intensity will be maximum for a black body is proportional to the fourth power of its absolute temperature.
View SolutionA black body A at a temperature of , emits radiant energy at the rate of 16 watt. Another black body B at temperature , emits radiant energy at the rate 8 watt in the same surrounding. Compare the surface areas of A and B.
View SolutionIf the temperature of a black body is increased by then the amount of radiant energy given out :
View SolutionWhich of the following curves represents spectral distribution of energy of black body radiation ?
View Solution