A particle of mass 1 g moves along the x-axis under the influence of two forces: i a force of attraction toward origin which is numerically equal to 4x dynes and ii a damping force whose magnitude in dynes is numerically equal to twice the instantaneous speed. Assuming that the particle starts from rest at a distance 10 cm from the origin a set up the differential equation of motion of the particle b find the position of the particle at any time c determine the amplitude period and frequency of the damped oscillation and d find the logarithmic decrement of the problem.
a The differential equation for the motion of the particle isThis is an example where the motion is damped oscillation b = 1 ω = 2 and b < ω. b The solution of this equation isc Amplitude = 20/√3e-t cm. The amplitudes of oscillation decrease towards zero as t increases.d From Eqn. 3.12 the logarithmic decrement δ is given by
Related Solutions
A particle of mass m moves on positive x-axis under the influence of force acting towards the origin given by If the particle starts from rest at the speed it will attain when it crosses the origin is
View SolutionA particle of mass m moves on positive x-axis under the influence of force acting towards the origin given by If the particle starts from rest at the speed it will attain when it crosses the origin is
View SolutionA particle of mass m moves on the x-axis under the influence of a force of attraction towards the origin O given by F=-(k)/(x^(2))hat(i) . If the particle starts from rest at x = a. The speed of it will attain to reach at distance x from the origin O will be
View SolutionA particle of mass m moves on the x-axis under the influence of a force of attraction towards the origin O given by F=-(k)/(x^(2))hat(i) . If the particle starts from rest at x = a. The speed of it will attain to reach at distance x from the origin O will be
View Solutionदो बलों जिनमें प्रत्येक का संख्यात्मक मान 10 डाइन के बराबर है चित्र में दर्शाये अनुसार लग रहे हैं। इन दोनों बलों का परिणामी ज्ञात कीजिए।
View SolutionA particle of mass m moves on the x-axis under the influence of a force of attraction towards the origin O given by . If the particle starts from rest at x = a. The speed of it will attain to reach at distance x from the origin O will be
View SolutionA particle starts from rest from origin and moves along a parabolic path whose equation is in the presence of a number of forces.One of the forces acting on the particle is .Find work done by this force F when the particle moves from origin to x=2m.
View SolutionA force of 4 dynes is present on a particle of mass 4g on X-axis. If it is at rest at x = 10cm initially, the equation for its motion is
View SolutionTwo force each numerically equal to 10 dynes are acting as shown in the figure, then find resultant of these two vectors.
View SolutionTwo force each numerically equal to 10 dynes are acting as shown in the figure, then find resultant of these two vectors.
View SolutionTwo force each numerically equal to 10 dynes are acting as shown in the figure, then find resultant of these two vectors.
View SolutionTwo force each numerically equal to 10 dynes are acting as shown in the figure, then find resultant of these two vectors.
View SolutionTwo forces , each numerically equal to 10 dyne are acting as shown in the following figure Their resultant is :
View SolutionTwo forces each numerically equal to 10 dynes are acting as shown in the following figure, then their resultant is -
View SolutionTwo forces , each numerically equal to 10 dyne are acting as shown in the following figure Their resultant is :
View SolutionA particle of mass m starts moving from origin along a horizontal x-y plane under the influence of a force of constant magnitude F ( which is always parallel to the x-axis ) and a constraint force. The trajectory of its motion is f ( x) = ( x)/( x^(2) + 1) . Then,
View SolutionA particle of mass m starts moving from origin along a horizontal x-y plane under the influence of a force of constant magnitude F ( which is always parallel to the x-axis ) and a constraint force. The trajectory of its motion is f ( x) = ( x)/( x^(2) + 1) . Then,
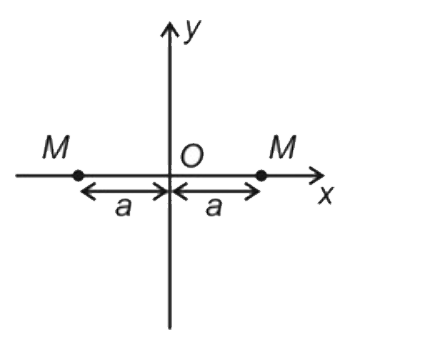
View SolutionTwo point masses M are kept fixed on the x-axis at a distance a from the origin, another point mass m is moving in a circular path of radius R (in y - z plane) under the influence of gravitational force of attraction, then speed of m will be (Assume no forces are acting on m other than the gravitational forces by two M)
View SolutionTwo point masses M are kept fixed on the x-axis at a distance a from the origin, another point mass m is moving in a circular path of radius R (in y - z plane) under the influence of gravitational force of attraction, then speed of m will be (Assume no forces are acting on m other than the gravitational forces by two M)
View SolutionThree forces are placed on the X-axis. 300 g At the origin of the force of, 500 g Force of x = 40 cm On and on 400 g Force of x = 70 cm Is kept at, then the distance of the mass-center from the point of origin .......
View Solution