Two masses m1 and m2 connected by a light spring of natural length l is compressed completely and tied by a light thread. This system while moving with velocity v along the positive x-axis passes through the origin at time t = 0. At this position the thread snaps. Find the positions of two masses as functions of time for t m 0.
Suppose x1 and x2 are the positions of two masses m1 and m2 at time t. The differential equations satisfied by x1 and x2 arewhere k is the spring constant of the spring. From these two equations we getWe know that the centre of mass moves with velocity V.
Related Solutions
Two masses m_(1) and m_(2) connected by a light spring of natural length l_(0) is compressed completely and tied by a string. This system while moving with a velocity v_(0) along +ve x -axis pass through the origin at t=0 . At this position the string snaps. Postion of mass m_(1) at time t is given by the equation. x_(1) (t)=v_(0)t-A(1-cosomegat) calculate : (a) Position of the particle m_(2) as a function of time. (b) l_(0) in terms of A .
View SolutionTwo masses and concute a high spring of natural length is compressed completely and tied by a string. This system while conving with a velocity along x-axis pass thorugh the origin at , at this position the string sanps, Position of mass at time t is given by the equation . Calculate (i) position of the particle as a funcation of time, (ii) in terms of A.
View SolutionTwo masses and concute a high spring of natural length is compressed completely and tied by a string. This system while conving with a velocity along x-axis pass thorugh the origin at , at this position the string sanps, Position of mass at time t is given by the equation . Calculate (i) position of the particle as a funcation of time, (ii) in terms of A.
View SolutionTwo point masses and are connected by a spring of natural length . The spring is compressed such that the two point masses touch each other and then they are fastened by a string. Then the system is moved with a velocity along positive x-axis. When the system reached the origin, the string breaks . The position of the point mass is given by where A and are constants. Find the position of the second block as a function of time. Also, find the relation between A and .
View SolutionTwo point masses and are connected by a spring of natural length . The spring is compressed such that the two point masses touch each other and then they are fastened by a string. Then the system is moved with a velocity along positive x-axis. When the system reached the origin, the string breaks . The position of the point mass is given by where A and are constants. Find the position of the second block as a function of time. Also, find the relation between A and .
View SolutionTwo point masses m_1 and m_2 are connected by a spring of natural length l_0 . The spring is compressed such that the two point masses touch each other and then they are fastened by a string. Then the system is moved with a velocity v_0 along positive x-axis. When the system reached the origin, the string breaks (t=0) . The position of the point mass m_1 is given by x_1=v_0t-A(1-cos omegat) where A and omega are constants. Find the position of the second block as a function of time. Also, find the relation between A and l_0 .
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0. Find the velocity vector and position vector of the particle vec v (t) and vec r (t) in relation with time.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0. Find the velocity vector and position vector of the particle vec v (t) and vec r (t) in relation with time.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
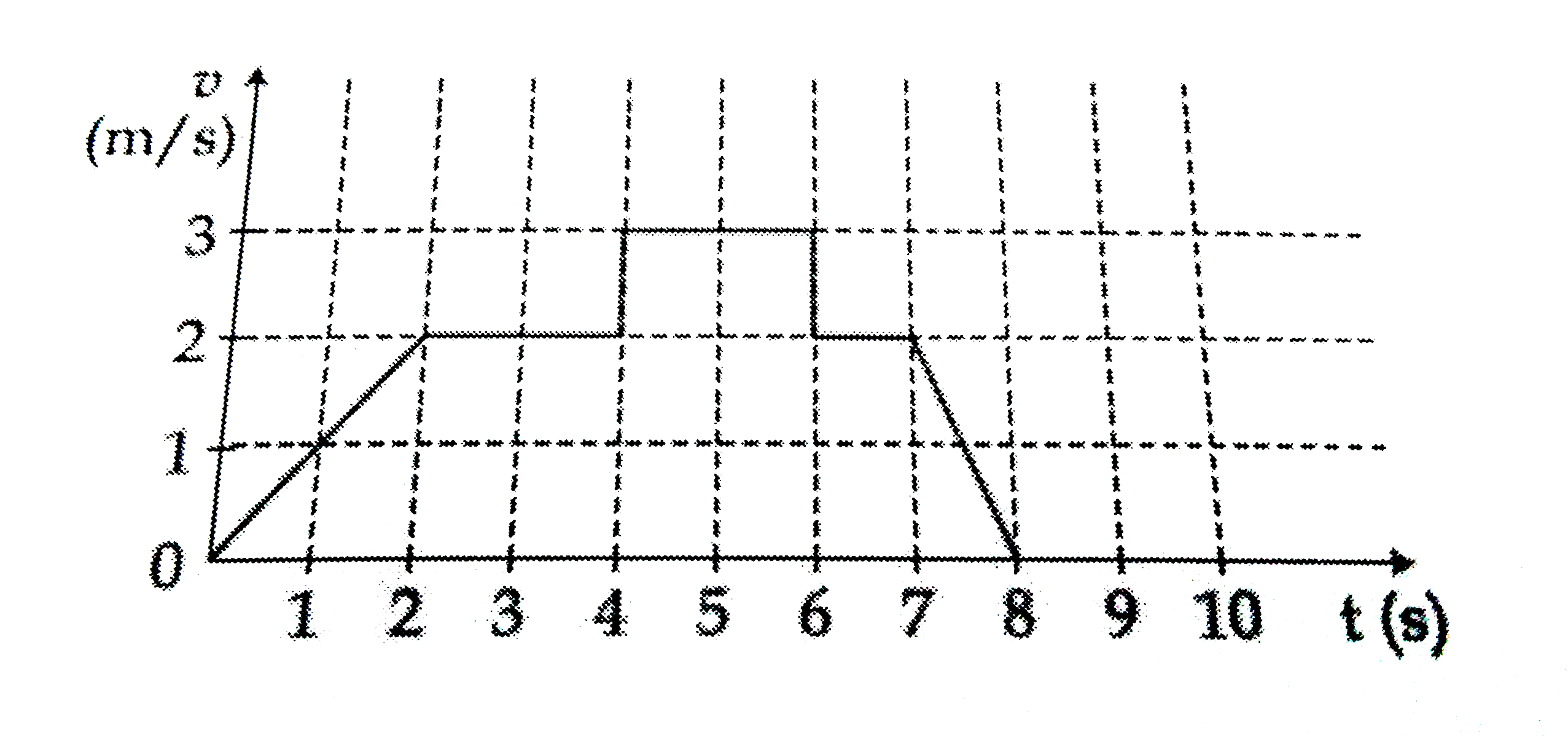
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
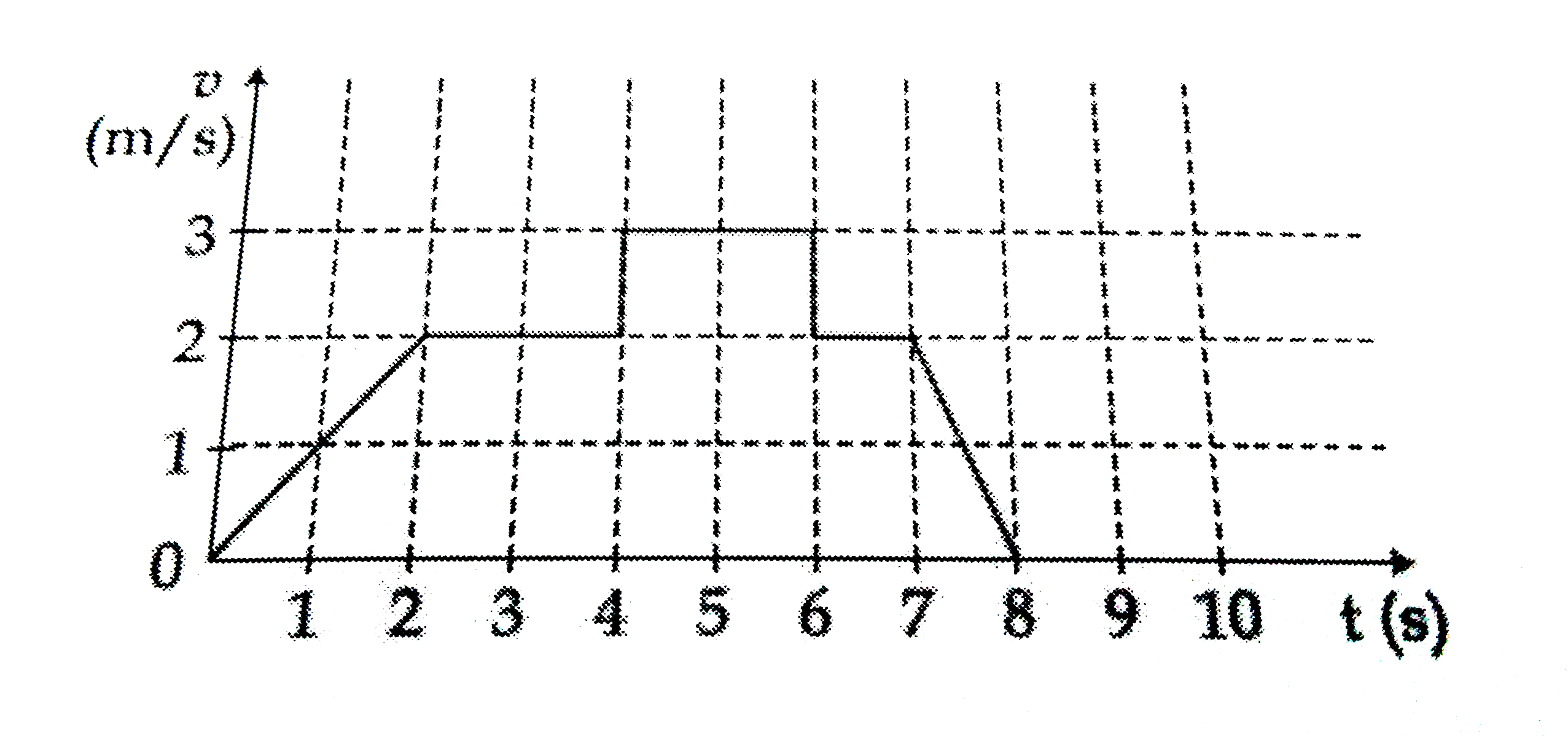
View SolutionTwo block-spring mass system are moving on smooth horizontal surface as shown in the figure as t=0. find out the minimum time t when the spring is maximum elongated l_(0) is the natural length of spring.
View SolutionThe velocity of a block of mass 2kg moving along x- axis at any time t is givne by v=20-10t(m//s) where t is in seconds and v is in m//s . At time t=0 , the block is moving in positive x- direction. The Kinetic energy of block at t=3 sec. is :
View SolutionThe velocity of a block of mass 2kg moving along x- axis at any time t is givne by v=20-10t(m//s) where t is in seconds and v is in m//s . At time t=0 , the block is moving in positive x- direction. The Kinetic energy of block at t=3 sec. is :
View SolutionThe velocity of a block of mass 2kg moving along x- axis at any time t is givne by v=20-10t(m//s) where t is in seconds and v is in m//s . At time t=0 , the block is moving in positive x- direction. The power due to net force on force on block at t=3 sec. is :
View SolutionThe velocity of a block of mass moving along axis at any time is givne by where is in seconds and is in . At time , the block is moving in positive direction.
The power due to net force on force on block at is
View SolutionA particle of mass m, moving in a circular path of radius R with a constant speed is located at point (2R, 0) at time t = 0 and a man starts moving with a velocity along the positive y-axis from origin at time t = 0. Calculate the linear momentum of the particle w.r.t. man as a function of time ______________.

View SolutionThe velocity of a particle moving along the positive direction of x-axis is v= Asqrt(x) , where A is a positive constant. At time t = 0 , the displacement of the particle is taken as x = 0 . (i) Express velocity and acceleration as functions of time , and (ii) find out the average velocity of the particle in the period when it travels through a distance s ?
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View Solution