Two concave mirrors equal radii of curvature R are fixed on a stand facing opposite directions. The whole system has a mass m and is kept on a frictionless horizontal table. Two blocks A and B each of mass m are placed on the two sides of the stand. At t =0 the separation between A and the mirror is 2R and also the separation between B and the mirror is 2R. The block B moves towards the mirror at a speed v. All collisions which take place are elastic. Taking the original position of the mirrors standard system to be x = 0 and x-axis along AB find the position of the image of A and B at; a t = R/v b t = 3R/v c t = 5R/v
a At t = R/v For block A u = -2R ∴ 1/v + 1/-2R = 2/-R or v = -2R/3 For block B: The distance travels by block B in time R/v is R Thus u = -R 1/v + 1/-R = 2/-R or v= -RThe x- coordinate of the image of the block with respect to the mirror will be +R b At t = 3R/v The block B will collide with the stand after time 2R/v. After collision block B becomes at rest and mirror starts moving with the same velocity v. In the remaining time R/v the distance moved by the mirror is R. The position of blocks and mirror are shown in fig. b At this time the blocks lie at the centre of curvature of the respective mirrors. Their images will form at the centres of curvature. So their coordinates are: For block A x = -R For block B x = +R c At t = 5R/v The block B will collide to the mirror after a time 2R/v thereafter mirror starts moving towards block A with velocity v At t = 4R/v the mirror will collide with block A and stops after collision. The positions of blocks and mirror are shown in fig. c For block A: Its image will form on the same place. Therefore the positions of the blocks are xA = -3R For block B: u = -2R 1/v + 1/-2R = 2/-R v = -2R/3 The co-ordinates of B : – 2R-2R/3 = -4R/3
Related Solutions
Two concave mirrors of equal radii of curvature R are fixed on a stand facing opposite directions. The whole system has a mass m and is kept on a frictionless horizonal table.
Two blocks A and B, each of mass m, are placed on the two side of the stand. At t=0, the separation between A and the mirrors is 2R and also the separation between B and the mirrors is 2R. The block B moves towards the mirror at a speed v. All collisions which take place are elastic. Taking the original position of the mirrors stand system to be x=0 and X -axis along AB, find the position of the image of A and B at t=
a.), b.) c.)
View SolutionTwo concave mirrorsof equal radi of curvature R are fixed on a stand facing opposite directions. The whole system has a mass m nd is kept onn a frictionlesss horiztonal table figure

Two blocks A and B, each of mass m, are placed on the two side of the stnd. At t=0, teh separation between A and the mirrors is 2R and also the separation between B and the mirrors is 2R. The block B moves towards the mirror at a speed v. All collisions which take place are erastic. Taking the original position of the mirrors stand system to be x=0 and X -axis along AB, find the position of the image of A and B at t=
, b. c.
View SolutionA Convex mirror of radius of curvature R is fixed on a standat rest with total mass m which is facing a block of equal mass m as shown in figure and is kept on a frictionless horizontal surfece. The separation between the block and mirror is 2R and block is moving at a speed v toward the mirror. Consider elastic collision between block and stand, find the speed of image after time 3R//v .
View SolutionA small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time (b) at a time .
View SolutionA small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time (b) at a time .
View SolutionA small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time (b) at a time .
View SolutionA small block of mass m and a concave mirror of radius R fitted with a stand, lie on la smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t=0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collides is perfectly elastic. Find the velocity of the image (a) at a time (b) at a time .
View SolutionA small block of mass m and a concave mirror of radius R fitted with a stand, lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t < dV (b) at a time t > d/V.
View SolutionAn object is placed exactly mid-way between a concave mirror and a convex mirror. The radius of curvature for each of them is 0.2 m. The mirrors are placed face to face and are 0.3 m apart. Find the position of the image formed by two successive reflections, the first one taking place at the concave mirror and then at the convex mirror.
View SolutionAn object of mass m is moving with velocity ữ towards a plane mirror kept on a stand as shown in the figure. The mass of the mirror and stand system is m. A head- on elastic collision takes place between the object and the mirror stand the velocity of image before and after the collision is
View SolutionTwo blocks of masses and are placed on a smooth horizontal surface as shown in the figure. Find the acceleration of each block and normal reaction between two blocks if a horizontal force is applied on (a) and (b)

View SolutionTwo blocks A and B of masses m and 2m respectively, attached at opposite ends of a spring of constant K, placed on a smooth horizontal surface. Spring is initially at its natural length l. A is given a velocity and B given velocity as shown.
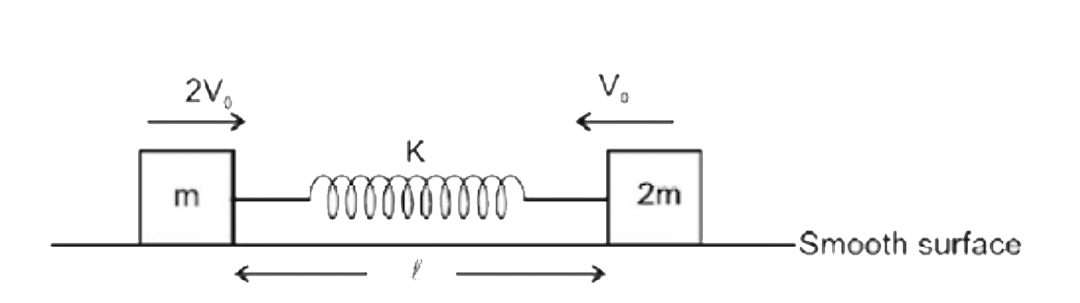
Maximum separation between m and centre of mass of the system will be :
View SolutionA point source of light is placed at the midpoint of two concave mirror (facing each other) of focal length f , What should be the magnitude of the distance of separation d between the two mirrors for a single image to be formed?
View SolutionA block of mass is placed on another block of mass which itself is lying on a horizontal surface .The coefficient of friction between two blocks is and that between the block of mass and horizontal surfece is What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA block of mass is placed on another block of mass which itself is lying on a horizontal surface .The coefficient of friction between two blocks is and that between the block of mass and horizontal surfece is What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA convex mirror of radius of curvature 70 cm and a plane mirror are placed face. The distance of separation between the mirrors is 28 cm. If a point source is placed on the principal axis in between the mirrors, two images are formed in the plane mirror. Determine the distance of the two images from the plane mirror.
View SolutionTwo blocks of masses M_1 and M_2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M, what is the contact force between the two blocks?
View SolutionTwo concave mirrors are placed facing each other and have the same centre of curvature. Where will the images of the point source Kept at this common centre of curvature be formed?
View SolutionWhat is the force of attraction between two masses each of 1 kg kept at a separation of 1 m?
View SolutionGravitational force between two point masses m and M separated by a distance r is F. Now if a point mass 3m is placed next to m, what will be the (a) Force on M due to m (b) total force on M ?
View Solution