A small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t<dV, (b) at a time t>dV. Solution in Tamil
The correct Answer is:A, B, D
a. At time t=t,
uy=−(d−Vt)
Here d>Vt,t=−R2
By mirror fomula 1v+1u=1f

→1v=1f−1u=−1R+1d−Vt
=−2(d−Vt)+RR(d−Vt)
v=−R(d−Vt)R−2(d−Vt)
differentiating w.r.t 't'
dvdt=−RV[R−2(d−Vt)]−2V[R(d−Vt)][R−2d(d−Vt)]2
=−R2V[R−2(d−Vt)]2
This is the required speed of mirror.
b. similar as above using u=(d−Vt).
Topper's Solved these Questions
Similar Questions
If the light moving in a straight line bends by a small but fixed angle it may be a case of
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
View SolutionA particle is moving at a constant speed V from a large distance towards a concave mirror of radius R along its principal axis. Find the speed of the image formed by the mirror as a function of the distance x of the particle from the mirror.
View SolutionTwo concave mirrorsof equal radi of curvature R are fixed on a stand facing opposite directions. The whole system has a mass m nd is kept onn a frictionlesss horiztonal table figure

Two blocks A and B, each of mass m, are placed on the two side of the stnd. At t=0, teh separation between A and the mirrors is 2R and also the separation between B and the mirrors is 2R. The block B moves towards the mirror at a speed v. All collisions which take place are erastic. Taking the original position of the mirrors stand system to be x=0 and X -axis along AB, find the position of the image of A and B at t=
a.Rυ, b. 3Rυ c. 5Rυ
View SolutionAn object is moving towards a convex mirror with a constant velocity. P is the pole of mirror.
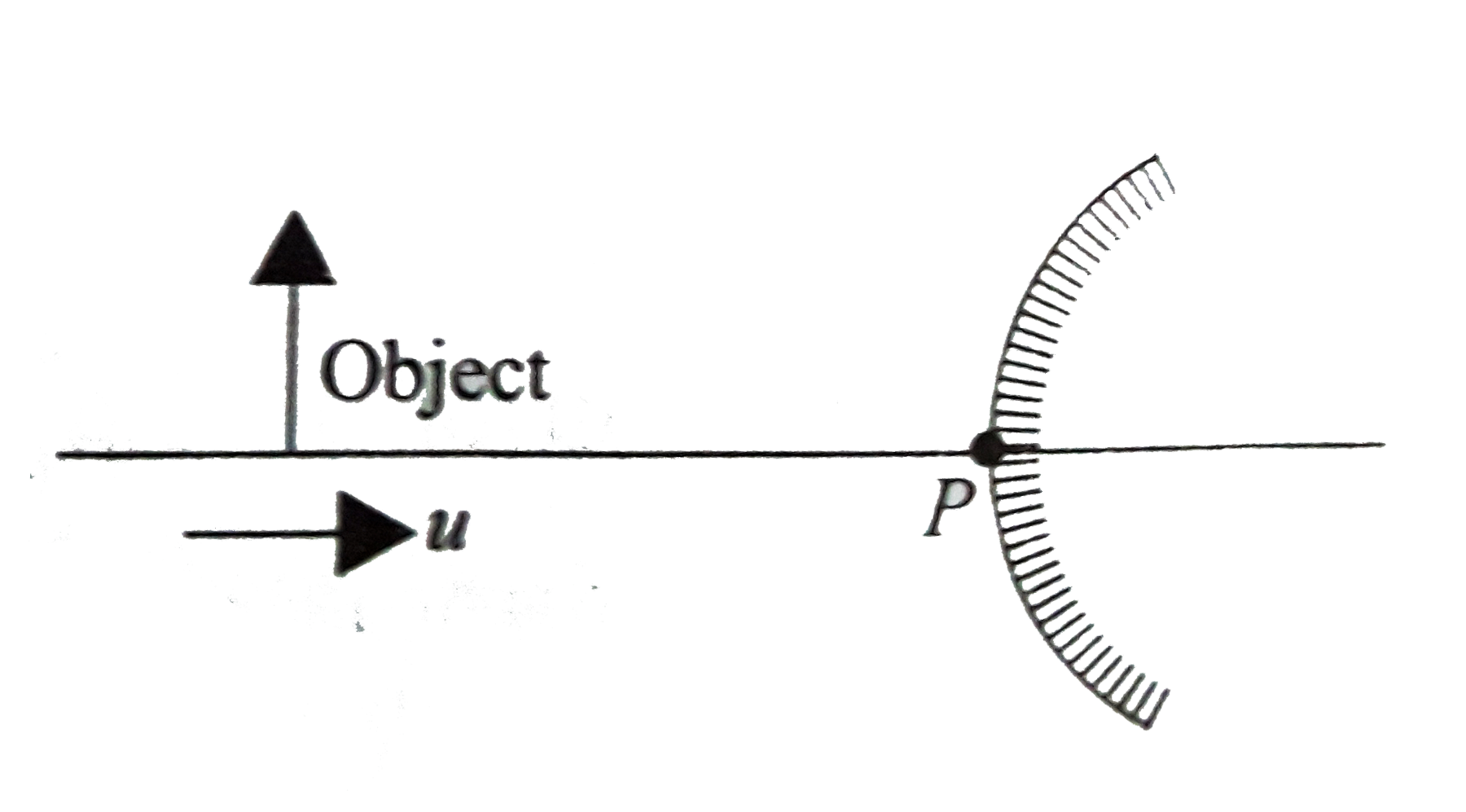
View SolutionA Convex mirror of radius of curvature R is fixed on a standat rest with total mass m which is facing a block of equal mass m as shown in figure and is kept on a frictionless horizontal surfece. The separation between the block and mirror is 2R and block is moving at a speed v toward the mirror. Consider elastic collision between block and stand, find the speed of image after time 3R//v .
View SolutionWhat will be the image speed if (i) Object is moving towards the plane mirror with speed v ? (ii) The plane mirror is moving towards the object with speed v ?
View Solutionकिसी घर्षणहीन पृष्ठ पर v चाल से चलता हुआ m द्रव्यमान का एक ब्लॉक, उसी द्रव्यमान m के विरमावस्था में स्थित एक अन्य ब्लॉक से टकराता है। टक्कर के पश्चात पहला ब्लॉक , v/3 चाल से, अपनी प्रारम्भिक गति की दिशा से θ कोण पर चलने लगता है। तो, टक्कर के पश्चात दूसरे ब्लॉक की चाल होगी :
View SolutionA block of mass M=4kg is moving with velocity V=6m/s toward a target block of mass=2kg, which is stationary (v=0). The object collide heat-on, and immediately after the collision, the speed of block m is 4 times the speed of block M.
Q. What is the speed of block M after the collision?
View SolutionA block of mass M=4kg is moving with velocity V=6m/s toward a target block of mass=2kg, which is stationary (v=0). The object collide heat-on, and immediately after the collision, the speed of block m is 4 times the speed of block M.
Q. Is the collision elastic?
View SolutionAn object of mass m is moving with velocity ữ towards a plane mirror kept on a stand as shown in the figure. The mass of the mirror and stand system is m. A head- on elastic collision takes place between the object and the mirror stand the velocity of image before and after the collision is
View Solutionएक मनोरंजन पार्क में लगे अवतल दर्पण की वक्रता त्रिज्या 4 cm है। एक बालिका दर्पण के सामने खड़ी है ताकि यह अपनी वास्तविक लम्बाई की 1.5 गुनी प्रतीत होती है। यदि प्रतिबिम्ब सीधा है तो यह दर्पण से कितनी दुरी पर खड़ी है।
View Solutionएक मनोरंजन पार्क में लगे अवतल दर्पण की वक्रता त्रिज्या 4 m है। एक बालिका दर्पण के सामने खड़ी है ताकि यह अपनी वास्तविक लम्बाई की 2.5 गुनी प्रतीत होती है। यदि प्रतिबिंब सीधा है तो यह दर्पण से कितनी दूरी पर खड़ी है ?
View SolutionOn a frictionless surface, a block of mass M moving at a v speed collides with another block located at rest of the same mass M. The first block after the collision, v/3 Speed, from the direction of its initial speed theta Starts walking at an angle. So, after the collision the second block will move.
View SolutionA particle is moving at a constant speed V from a large distance towards a concave mirror of radius R along its principal axis. Find the speed of the image formed by the mirror as a function of the distance x of the particle from the mirror.
View Solution