The figure shows a process on a gas in which pressure and volume both change. The molar heat capacity for this process is C. Thena C = 0b C = Cvc C > Cvd C < Cv
Correct option c C > CvExplanation:According to graph pressure is increasing also volume is increasing hence T also increases. It means that energy is used both in increasing internal energy and work done nCdt = nCVdt +PΔV ∴ C > CV
Related Solutions
The molar heat capacity for the process shown in fig. is
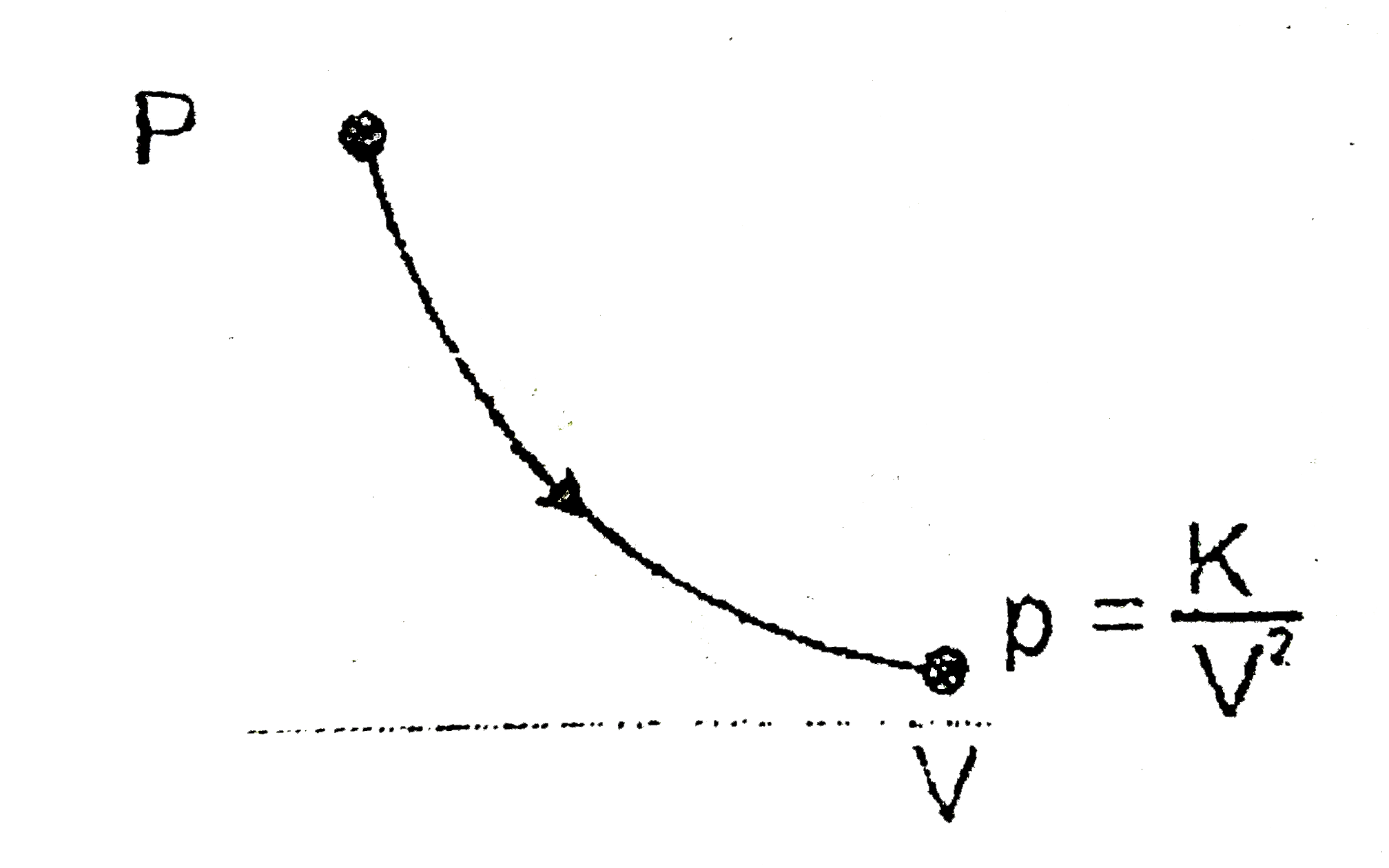
View SolutionFigure shows a process on a gas in which pressure and volume both change. The molar heat capacity for this process is C.
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionIf molar heat capacity of the given process (as shown in figure) is C , then
View SolutionIf molar heat capacity of the given process (as shown in figure) is C , then
View SolutionAn ideal gas is taken through a process in which pressure and volume vary as . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which pressure and volume vary as P = kV^(2) . Show that the molar heat capacity of the gas for the process is given by C = C_(v) +(R )/(3) .
View SolutionThe heat capacity of an ideal gas in a polytropic process is C=Cv+0.1R.The value of polytropic exponent is :
View SolutionAn ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View SolutionThe volume of a gas decreases from 500 c c to 300 c c when a sample of gas is compressed by an average pressure of 0.6 atm. During this process 10 J of heat is liberated. The change in internal energy is
View SolutionA gas has molar heat capacity C = 4.5 R in the process PT = constant . The number of degrees of freedom of molecules in the gas is
View SolutionAn ideal gas undergoes a process in which co-efficient of volume expansion of gas , varies with absolute temperature by the relation . Let C is molar heat capacity in this process and are molar heat capacities at constant pressure and volume respectively. Then
View SolutionAn ideal gas undergoes a process in which co-efficient of volume expansion of gas gamma , varies with absolute temperature by the relation gamma=(2)/(T) . Let C is molar heat capacity in this process and C_(p).C_(V) are molar heat capacities at constant pressure and volume respectively. Then
View SolutionThe molar heat capacity for an ideal gas a) is zero for an adiabatic process b) is infinite for an isothermal process c) depends only on the nature of the gas for a process in which either volume or pressure is constant d) is equal to the product of the molecular weight and specific heat capacity for any process
View SolutionThe molar heat capacity for an ideal gas a) is zero for an adiabatic process b) is infinite for an isothermal process c) depends only on the nature of the gas for a process in which either volume or pressure is constant d) is equal to the product of the molecular weight and specific heat capacity for any process
View SolutionA gas undergoes a process such that . If the molar heat capacity for this process is , find the degree of freedom of the molecules of the gas.
View SolutionA gas undergoes a process such that pprop1/T . If the molar heat capacity for this process is C=33.24J//mol-K , find the degree of freedom of the molecules of the gas.
View Solution