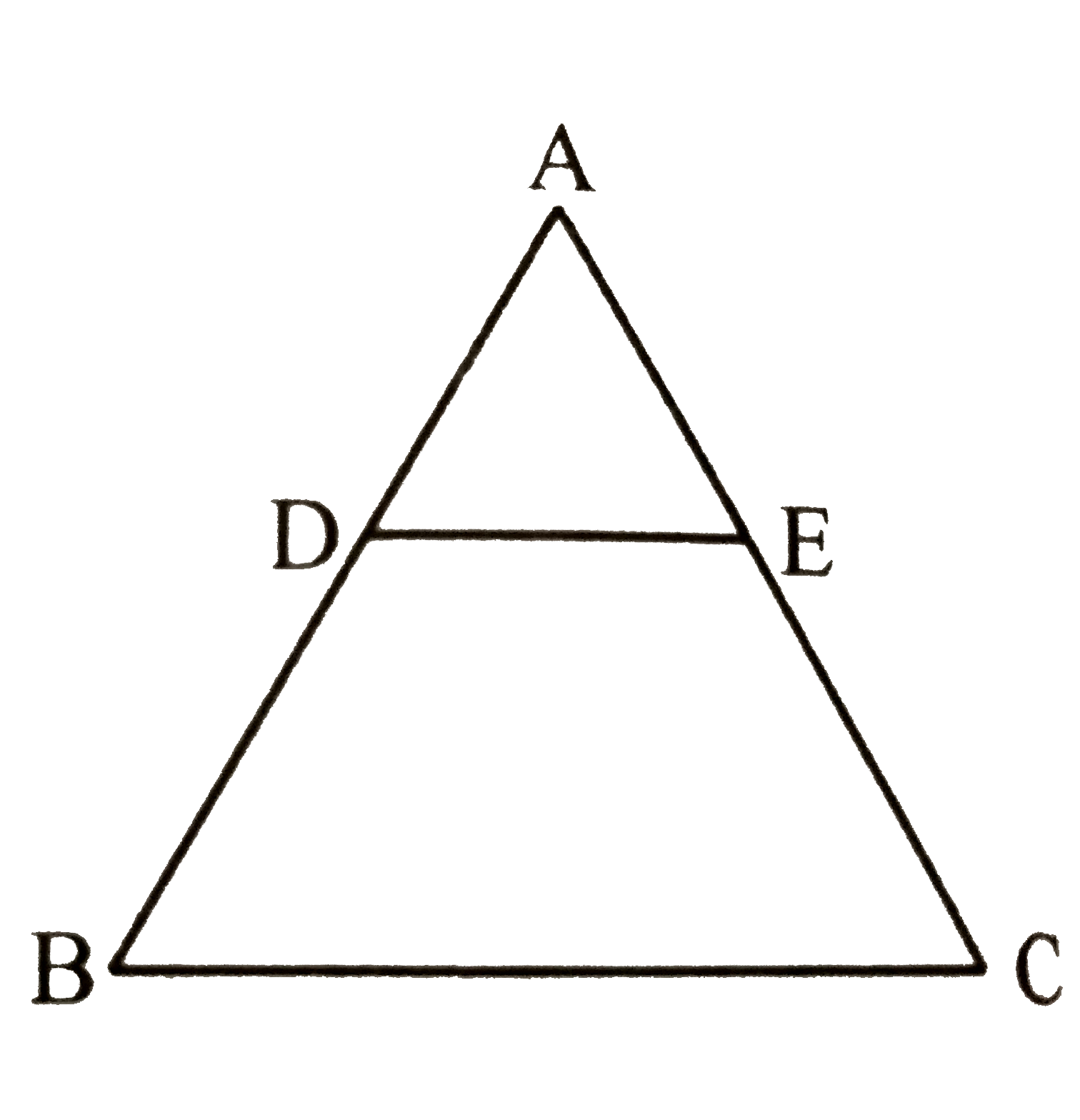
D and E are points on the sides AB and AC respectively of a triangle ABC such that DE is parallel to BC and divides triangle ABC into two parts equal in area. Prove that BD/AB=2-sq.rt of 2/2
Solution:Given: ABC is a triangle with DE || BC divides the triangle into two parts equal in areas.To find: BD/AB=2-sq.rt of 2/2Area of ΔADE = Area of Trapezium BDEC As given∴ Area of ΔADE = 1/2 area of ΔABC ------------1In ΔADE and ΔABC∠ADE = ∠ABC Corresponding angles∠AED = ∠ACB Corresponding anglesΔADE ∼ ΔABC AA similarity ∴ Area of ΔADE / Area of ΔABC = AD2/AB2 Areas of similar triangle --------2∴ From equation 1 and 2 we get=> 1/2 = AD2/AB2=> AD/AB = 1/√ 2∴ AB – AD = √ 2 AD – AD∴ BD = √ 2 – 1AD∴ BD/AB = √ 2 – 1AD / √ 2 AD∴ BD/AB = √ 2 – 1 / √ 2 --------------3Multiplying Nr and Dr of equation 3 by √ 2 we get∴ BD/AB = 2 – √ 2 / 2
Related Solutions
एक की भुजाओं AB तथा AC पर क्रमशः बिंदु D तथा E है | तथा और दो बराबर भागो के क्षेत्रफलो में बँटा हुआ है तो का मान ज्ञात कीजिए |
View Solutionमें, , तथा भुजाओं AB व AC पर क्रमशः D व E बिंदु हैं। यदि BD = EC हैं, तो सिद्ध कीजिए कि DE BC |
View Solutionएक की भुजाओं AB तथा AC पर क्रमशः बिंदु D तथा E है | तथा और BD = CE है | तो सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज है |
View SolutionIn the figure, D and E are the points on sides AB and AC of /_\ABC such that DE|\|BC. and divides △ABC into two parts, equal in area, Find AB BD .
View SolutionIn , D and E are two points on the sides AB and AC respectively so that DE || BC and . Then
View SolutionIn a triangle ABC, it is known that AB=AC. Suppose D is the mid-point of AC and BD=BC=2. Then the area of the triangle ABC is-
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of and area of .
Prove that
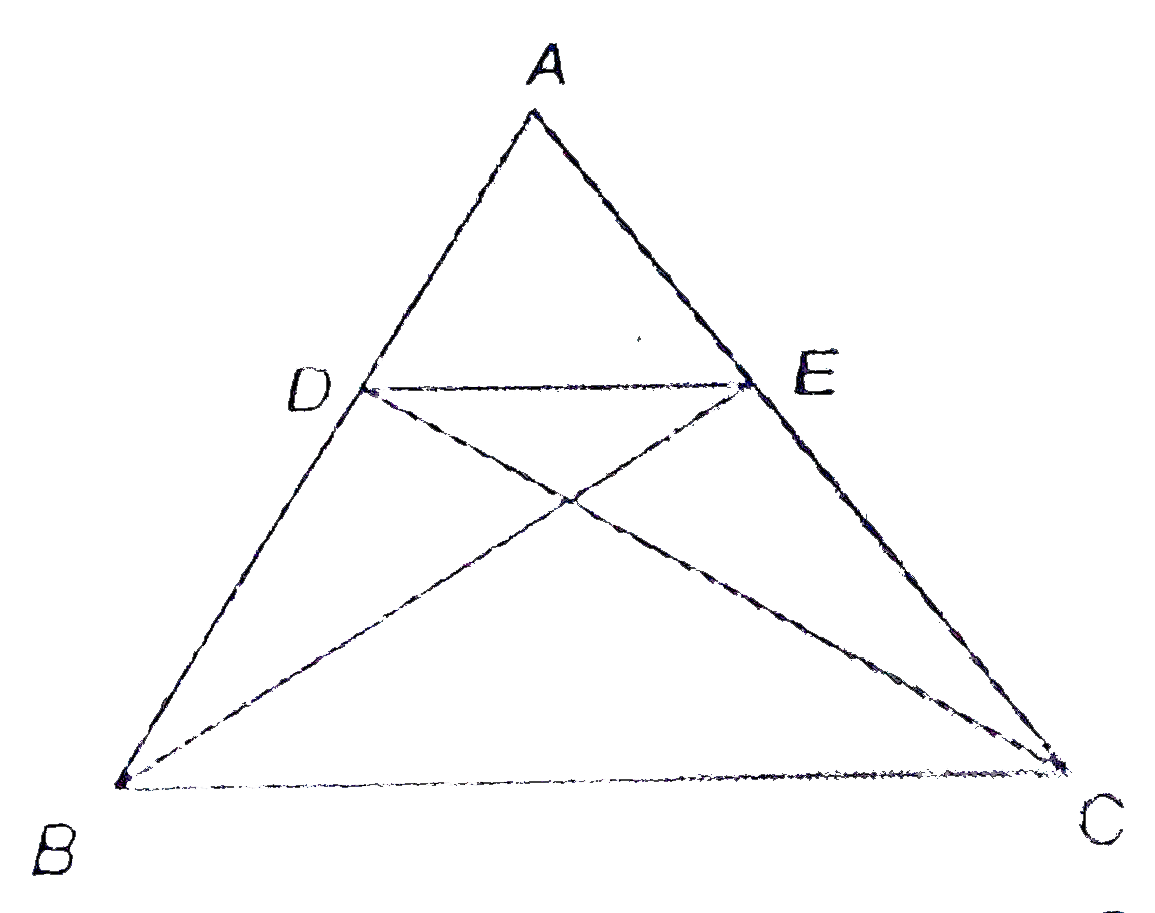
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of and area of .
Prove that

View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively such that DE || BC and 5 is 6. triangle The ratio of the area of ABC and that of trapezium DECB is:
View SolutionABC में D और E दो बिन्दु है जो क्रमशः भुजा AB और AC पर इस प्रकार है कि DECB समलंब (पोजियम) का क्षेत्रफल :ABC का क्षेत्रफल किसके बराबर होगा
View Solutionలో DE // BC మరియు D, E లు వరుసగా AB, AC లపై బిందువులైన
View SolutionD and E are points on sides AB and AC respectively of ABC such that ar (DBC) = ar EBC). Prove that DEBC.
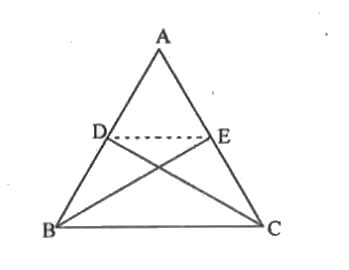
View Solutionत्रिभुज ABC की भुजा BC पर दो बिन्दु D तथा E इस प्रकार हैं कि BD=EC तथा AD=AE हो, तो सिध्द कीजिए कि AB=AC.
View SolutionOne Delta In ABC, point P cuts side AB in two parts and point side AC in two parts such that PQI|BC. PQ divides the triangle ABC into two parts which are equal in area. BP : AB will be
View SolutionDE॥ in a triangle ABC BC, in which D is a point on AB and E is a point on AC There are points. DE, /_\ Two equal areas of BAC divides into parts, then DE : AB Is equal?
View SolutionIn an isoscles is a point on BC. Prove that .
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
View Solutionएक त्रिभुज ABC है | जिसमे AB = AC तथा D, BC पर कोई बिंदु है | तो सिद्ध कीजिए कि
View Solutiontriangle In ABC, D and E are two points on the sides AB and BC respectively such that AD: DB = 2:3 and DE || There is AC. If triangle Area of ADE is 18 cm. Yes then triangle What is the area (in cm) of ABC?
View Solutionand are points on the sides and respectively of a such that and divides into two parts, equal in area, find .
View Solution