In the figure i an extensible string is fixed at one end and the other end is pulled by a tension T. In figure ii another identical string is pulled by tension T at both the ends. The ratio of elongation in equilibrium of string in i to the elongation of string in ii isA 1 : 1 B 1 : 2 C 2 : 1 D 0
Correct option A 1 : 1Explanation:Tension in both string shall be same which can be observed by making FBD of string in figure 1
Related Solutions
In the figure (i) a uniform string is fixed at one end and the other end is pulled by a tension T. another force T acts at mid point of the string. In figure (ii) another identical string is pulled by tension T at both the ends. The ratio of elongation in equilibrium of string (i) to the elongation of string in (ii) is
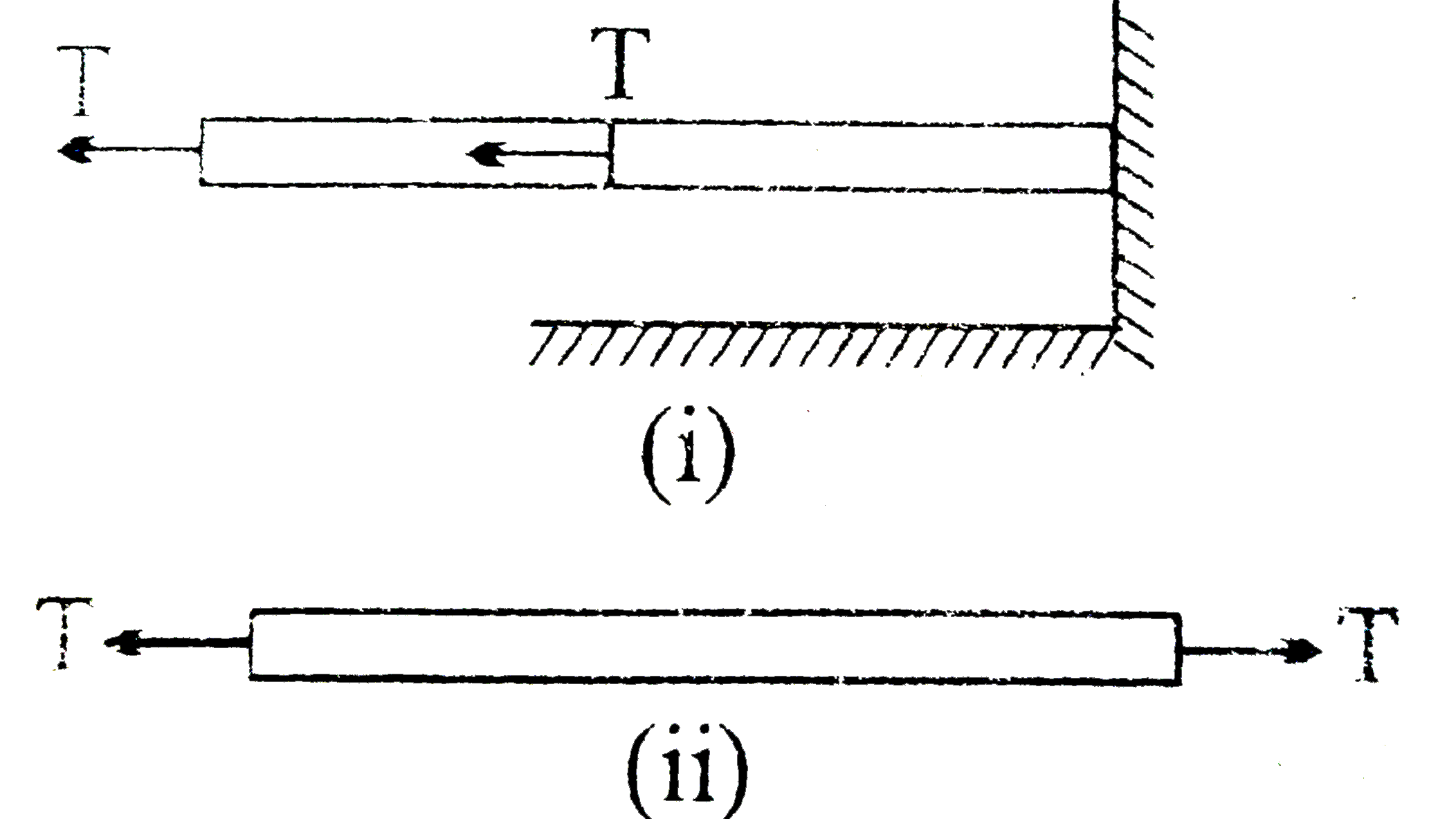
View SolutionIn the figure (i) an extensible string is fixed at one end and the other end is pulled by a tension T. In figure (ii) another identical string is pulled by tension T' at both the ends. The ratio of elongation in equilibrium of string in (i) to the elongation of string in (ii) is
View SolutionA string of lenth l fixed at one end carries a mass m at the other end. The strings makes around the axis through the fixed end as shown in the figure, the tension in the string is
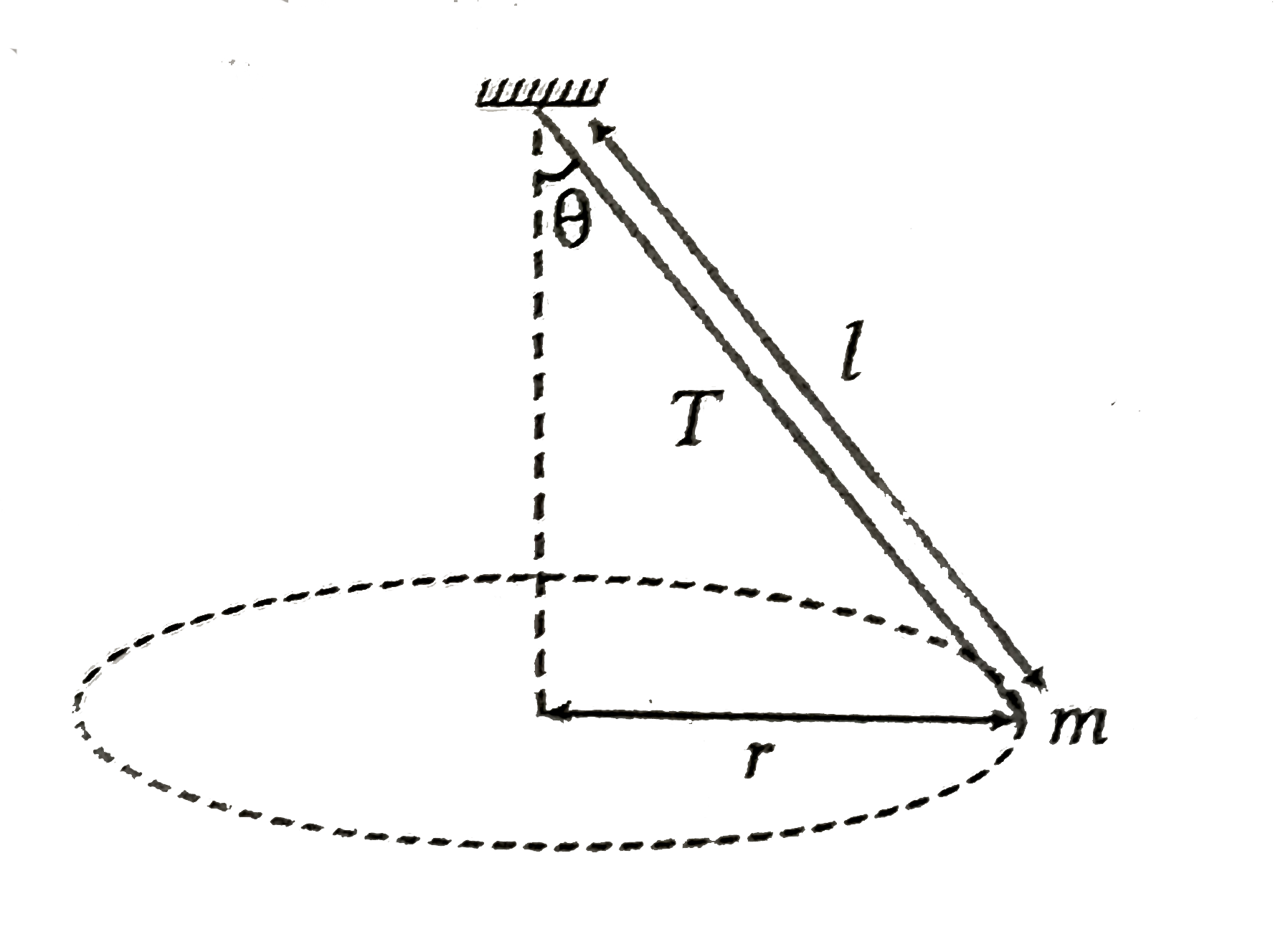
View SolutionA string of length l fixed at one end carries a mass at the other end. The strings makes around the axis through the fixed end as shown in the figure, the tension in the string is

View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
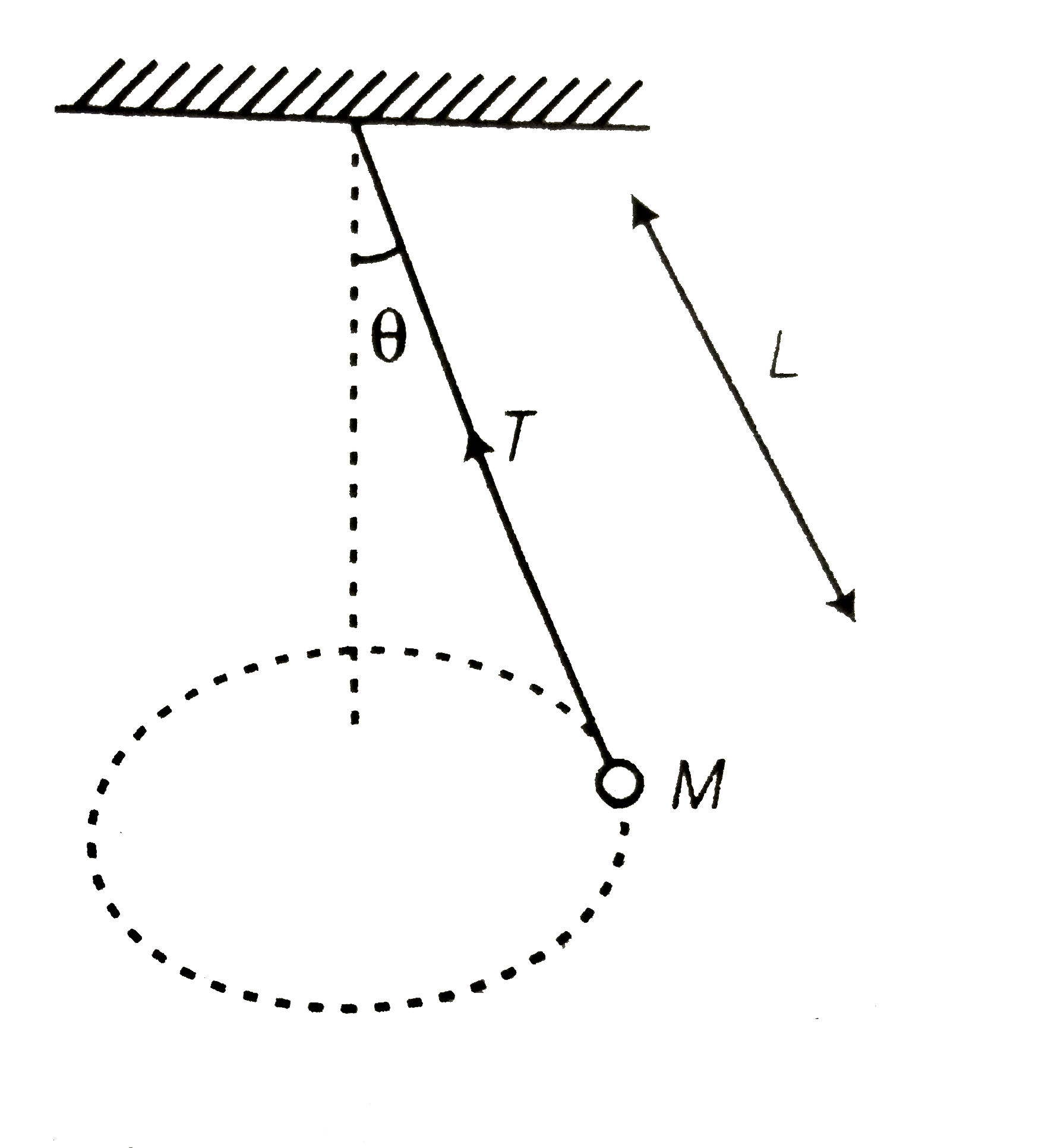
View SolutionA string of length L is fixed at one end and carries a mass M at the other end . The string makes revlutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes revolution per second around the vertical axis through the fixed end as shown in the figure, the tension in the string is :
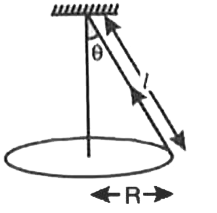
View SolutionA string of length is fixed at one end and carries a mass at the other end. The string makes revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

View SolutionA string of length 1m is fixed at one end and carries a mass of 1 kg at the other end. The string makes 2//pi revolutions per second around a vertical axis passing through the fixed end. Calculate (i) angle of inclination of the string with the vertical, (ii) the tension in the strong and (iii) the linear velocity of the mass.
View SolutionAs shown in Fig. (I), one end of a tensile rope is inertial. The other end is pulled by tension T. In Fig. (Ii) the second uniform rope is pulled by tension T from both ends. So the ratio of expansion of rope (i) to equilibrium (ii) in equilibrium will be -
View SolutionA string of mass per unit length is clamped at both ends such that one end of the string is at x = 0 and the other is at . When string vibrates in fundamental mode, amplitude of the midpoint O of the string is a, tension in a, tension in the string is T and amplitude of vibration is A. Find the total oscillation energy stored in the string.
View SolutionA string of mass per unit length is clamped at both ends such that one end of the string is at x = 0 and the other is at . When string vibrates in fundamental mode, amplitude of the midpoint O of the string is a, tension in a, tension in the string is T and amplitude of vibration is A. Find the total oscillation energy stored in the string.
View SolutionA string of mass per unit length mu is clamped at both ends such that one end of the string is at x = 0 and the other is at x =l . When string vibrates in fundamental mode, amplitude of the midpoint O of the string is a, tension in a, tension in the string is T and amplitude of vibration is A. Find the total oscillation energy stored in the string.
View SolutionA string of mass per unit length is clamped at both ends such that one end of the string is at and the other end is at x = l . When string vibrates in fundamental mode amplitude of the mid point O of the string is a and tension in the string is T . Find the total oscillation energy stored in the string .
View SolutionThe mass of the part of the string below A i figure is m. Find the tension of he string at the lowere end and at A.
View SolutionA string of mass and length , fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is and the tension in the string is . If the energy of vibrations of the string is . Find
View SolutionA string of mass 'm' and length l , fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T' . If the energy of vibrations of the string is (pi^(2)a^(2)T)/(etaL) . Find eta
View SolutionA string of mass and length , fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is and the tension in the string is . If the energy of vibrations of the string is . Find
View SolutionThe tension T in the string shown in figure is
View SolutionThe tension T in the string shown in figure is
View Solution