A rod ABCD has two different cross-sectional areas of 200mm2 and 100mm2 as shown in Fig. 1.51. The rod is held between two rigid supports at its ends. The loads P each act at sections B and C of the rod. If P = 20kN determine the axial stresses in each section of the rod.
Load P acts as a compressive force on rod BC and as a tensile force on rod AB such that the compressive force on rod BC is P - P1. Compatibility condition Extension in AB+ contraction in BC+ extension in CD = 0
Related Solutions
Two rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained . If temperature of system is increased by DeltaT then junction will not shift if -
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained . If temperature of system is increased by DeltaT then junction will not shift if -
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained . If temperature of system is increased by DeltaT then junction will not shift if -
View SolutionTwo rods of different metals, having the same area of cross-section A, are placed end to end between two massive walls as shown in fig. If the temperature of both the rods are now raised by Delta t^@ C then a) Find the force with which the rods acts on each other at higher temperature. b) Find the lengths of the rods at the higher temperature. Assume that there is no change in the cross-sectional area of the rods and the rods do not bend. There is no deformation of walls.
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram Ratio of elongation in section PQ of rod and section QR of rod is
View SolutionTwo blocks and of masses and are placed on a smooth horizontal surface. Block is given a speed of . Find
The maximum speed of
The minimum speed of .
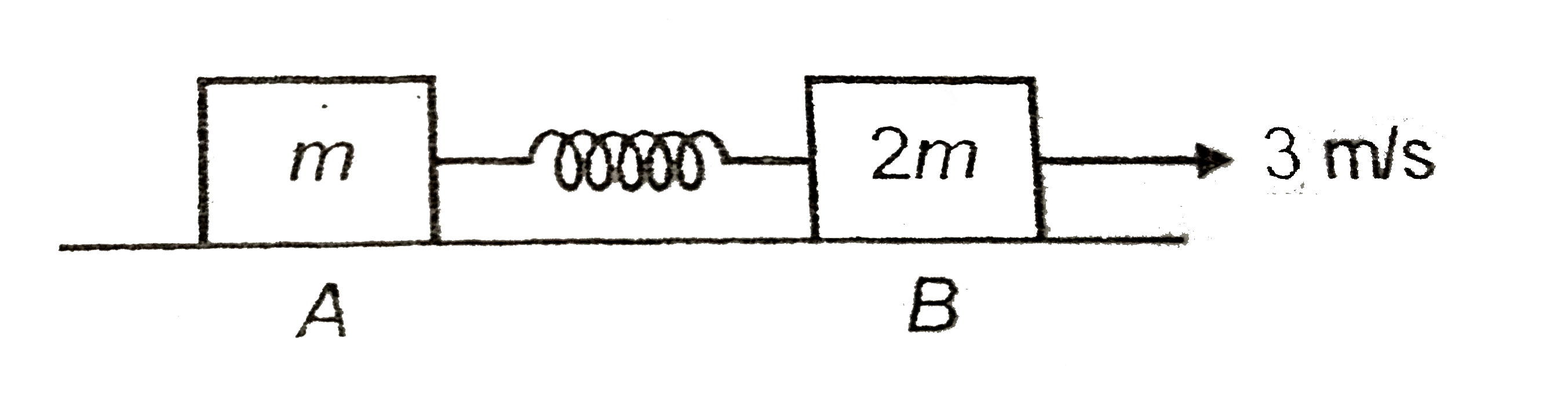
View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View SolutionForce is acting as shown on a rod. Total detail known taxes in rods. (E is the elasticity coefficient of the rod and A is the cross section of the rod.)
View SolutionTwo rods of different metals, having the same area of cross-section A, are placed end to end between two massive walls as shown in fig. If the temperature of both the rods are now raised by then
(a) Find the force with which the rods acts on cach other at higher temperature.
(b) Find the lengths of the rods at the higher temperature.
Assume that there is no change in the cross-sectional area of the rods and the rods do not bend. There is no deformation of walls.

View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_228_Q01.png)
If temperature of system is increased by then thermal stress developed in first rod-
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_228_Q01.png)
If temperature of system is increased by then thermal stress developed in first rod-
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_228_Q01.png)
If temperature of system is increased by then thermal stress developed in first rod-
View SolutionTwo rods of different metals, having the same area of cross-section A, are placed end to end between two massive walls as shown in fig. If the temperature of both the rods are now raised by then
(a) Find the force with which the rods acts on each other at higher temperature.
(b) Find the lengths of the rods at the higher temperature. Assume that there is so change in the corss-sectional area of the rods do not bend. There is no deformation of walls.

View Solutionएक भार की छड़ का एक सिरा एक दिवार से लटका है | उसके दूसरे सिरे पर भार लटका है | छड़ की अनुप्रस्थ काट का क्षेत्रफल A है, छड़ के मध्य बिन्दु पर प्रतिबल होगा
View SolutionA copper rod with length 1.4 m and area of cross-section of 2 cm^2 is fastened to a steel rod with length L and cross-sectional area 1 cm^2 . The compound rod is subjected to equal and opposite pulls to magnitude 6.00xx10^4 N at its ends . (a) Find the length L of the steel rod if the elongation of the two rods are equal . (b) What is stress in each rod ? (c ) What is the strain in each rod ? [Y_"steel"=2xx10^11 Pa , Y_(Cu)=1.1xx10^11 Pa]
View SolutionA copper rod with length 1.4 m and area of cross-section of 2 cm^2 is fastened to a steel rod with length L and cross-sectional area 1 cm^2 . The compound rod is subjected to equal and opposite pulls to magnitude 6.00xx10^4 N at its ends . (a) Find the length L of the steel rod if the elongation of the two rods are equal . (b) What is stress in each rod ? (c ) What is the strain in each rod ? [Y_"steel"=2xx10^11 Pa , Y_(Cu)=1.1xx10^11 Pa]
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram Ratio of elastic potential energy stored in section PQ and section QR of the rod is
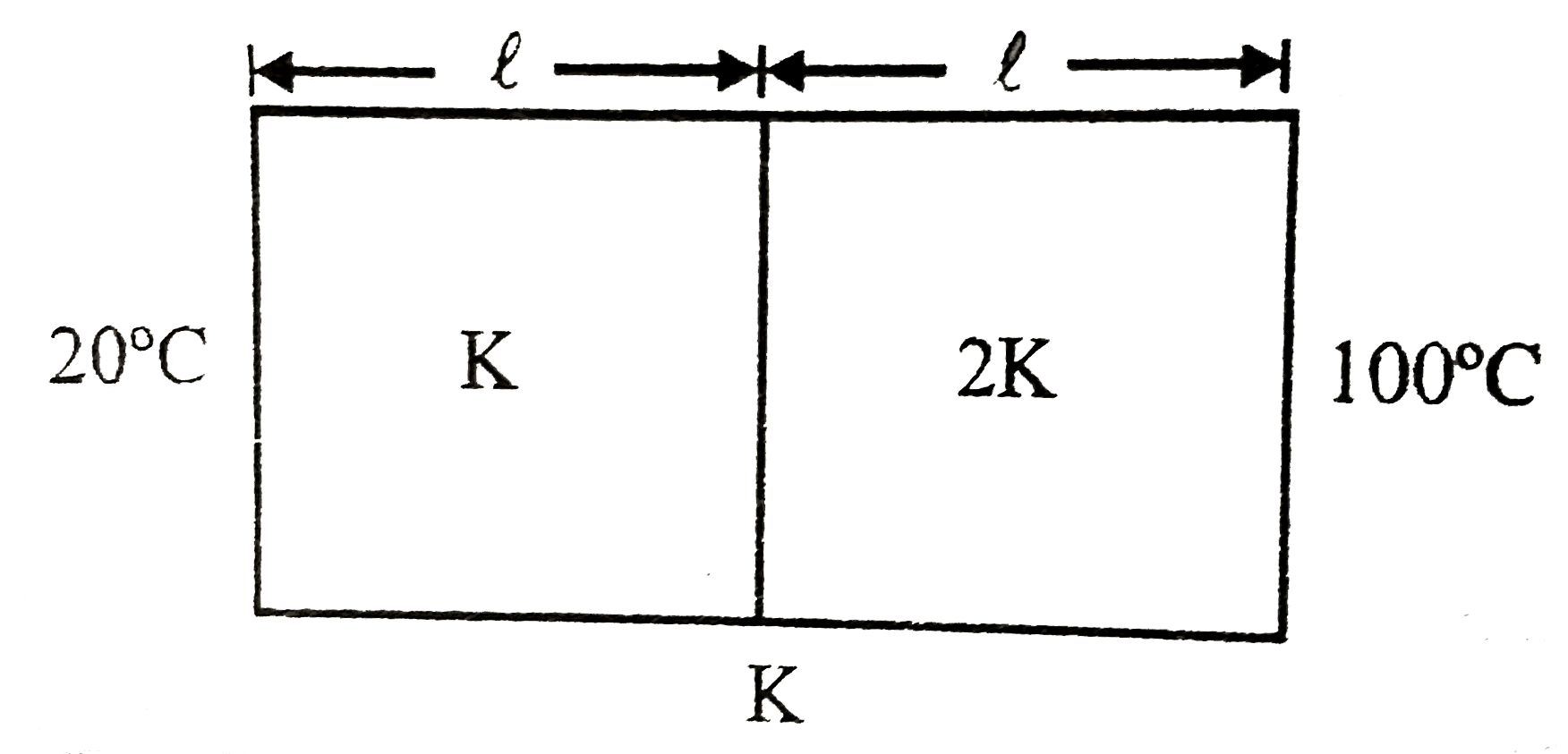
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature of the interface will be -
View SolutionEqual and opposite forces are applied on a rod as shown in the figure. From any cross-section of the plane PQRS rod theta makes an angle. If the area of cross section of the rod is 'A', then the tensile stress on PQRS will be
View SolutionTwo rods A and B have lengths l_1 and l_2. Each rod has its ends at temperature T_1 and T_2 Radii fo cross section of the two rods are same. The condition for equal flow of heat through those two rods is (K_1, K_2 are thermal conductivities of two rods)
View Solution