Two rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_228_Q01.png)
If temperature of system is increased by ΔT then thermal stress developed in first rod-
is equal to thermal stress developed in second rod
is greater than thermal stress developed in second rod
is less than thermal stress developed in second rod
None of these
The correct Answer is:A
As cross sectional area is same & equal and opposite force acting on both rods. So F/A = same
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 04 (A)
Explore 48 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 04 (B)
Explore 15 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:ASSERTION-REASON
Explore 40 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Two same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
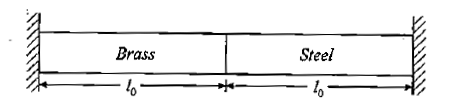
View SolutionA rod of length / and radius r is held between two rigid walls so that it is not allowed to expand. If its temperature is increased, then the force developed in it is proportional to
View Solution
Knowledge Check
Two rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_227_Q01.png)
If temperature of system is increased by ΔT then junction will not shift if -AY1α1=Y2α2BY1α1l1=Y2α2l2Cα1=α2DY2α1l2=Y1α2l2Two rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_229_Q01.png)
If temperature of system is increased by ΔT then shifting in junction if junction if Y1α1>Y2α2 is given by -Al1l2(Y1α2−Y2α1)Y1l1+Y2l2Bl1l2(Y1α1−Y2α2)Y1l2+Y2l1Cl1l2(Y1α1−Y2α2)Y1l1+Y2l2DNone of theseTwo rods of different materials and identical cross sectional area, are joined face to face at one end their free ends are fixed to the rigid walls. If the temperature of the surroundings is increased by 30∘C, the magnitude of the displacement of the joint of the rod is (length of rods l1=l2=1unit, ratio of their young's moduli, Y1/Y2=2, coefficients of linear expansion are α1 and α2)
A5(α2−α1)B10(α1−α2)C10(α2−2α1)D5(2α1−α2)
Three rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionTwo rods of different materials but having same length L and cross-sectioinal areas A are arranged end-to-end between fixed supports. The temperature is T and there is no initial stress. The rods are heated so that their temperature increases by ΔT. Find : (a) the displacement of the interface (b) the stress at the interface. The coefficinets of linear expansioin of the materials are α1 and α2 and their Young's modulii are E1 and E2 respectively.
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is

View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod is
View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View Solution

