An aluminium bar of a diameter of 10mm and a length of 400mm is rigidly held at its upper end. It is subjected to an axial force P = 12kN at section B as shown in Fig. 1.29. E for aluminium = 67kN/mm2. Gap between the lower end and the floor is 0.2mm. Determine the stresses in portions AB and BC of the bar.
Under the action of the force P the portion AB of the bar extends and the end C of the bar touches the floor. Then reaction offered from floor provides a compressive force for portion BC of bar. Say P1 = tensile force in portion AB P2 = compressive force in portion BC
Related Solutions
A bar is subjected lu axial forces as shown. is the modulus of elasticity of the bar is E and A is it cross-section area. Its elongation will be

View SolutionA bar is subjected to axial forces as shown. is the modulus of elasticity of the bar is E and A is it cross-section area. Its elongation will be
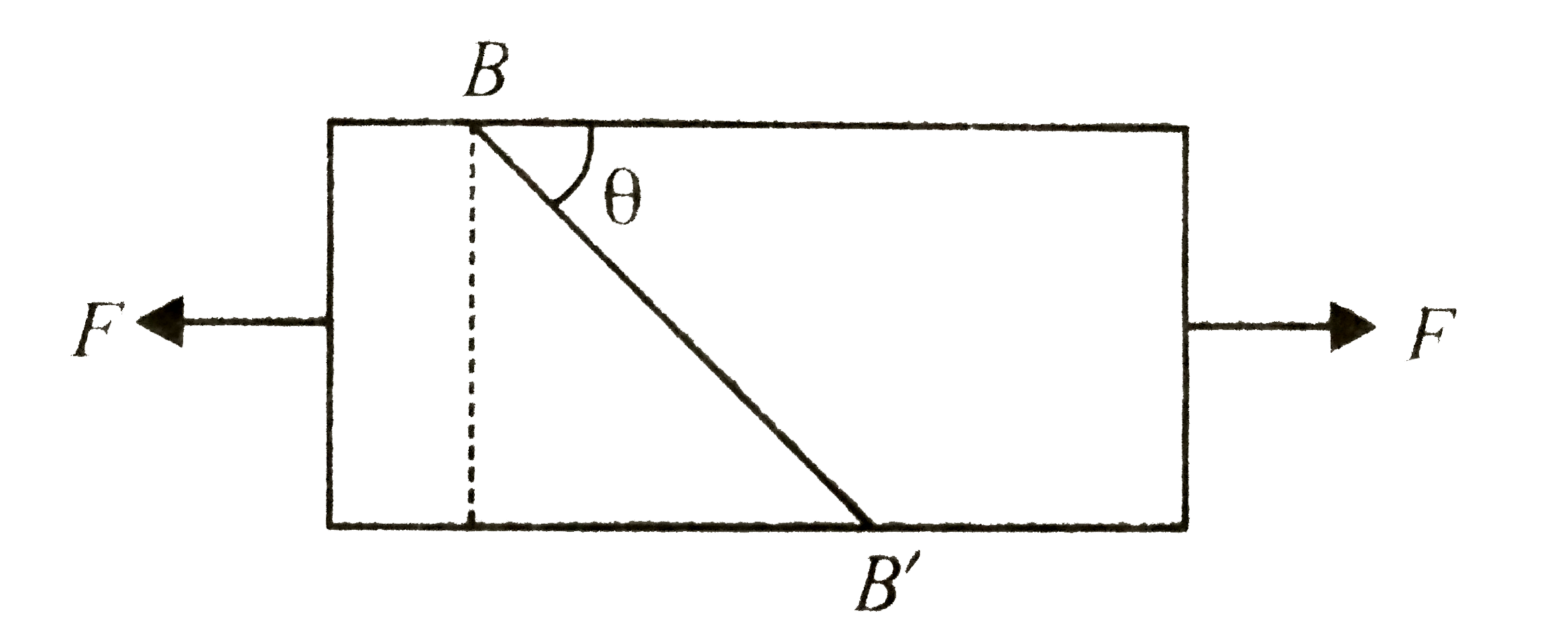
View SolutionA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle with length. The ratio of tensile stress to the shearing stress on the plane BB' is
View SolutionA rectangular bar is uniformly loaded axially with force per unit area shown. Shown is a section in the bar. Normal stress for the section is
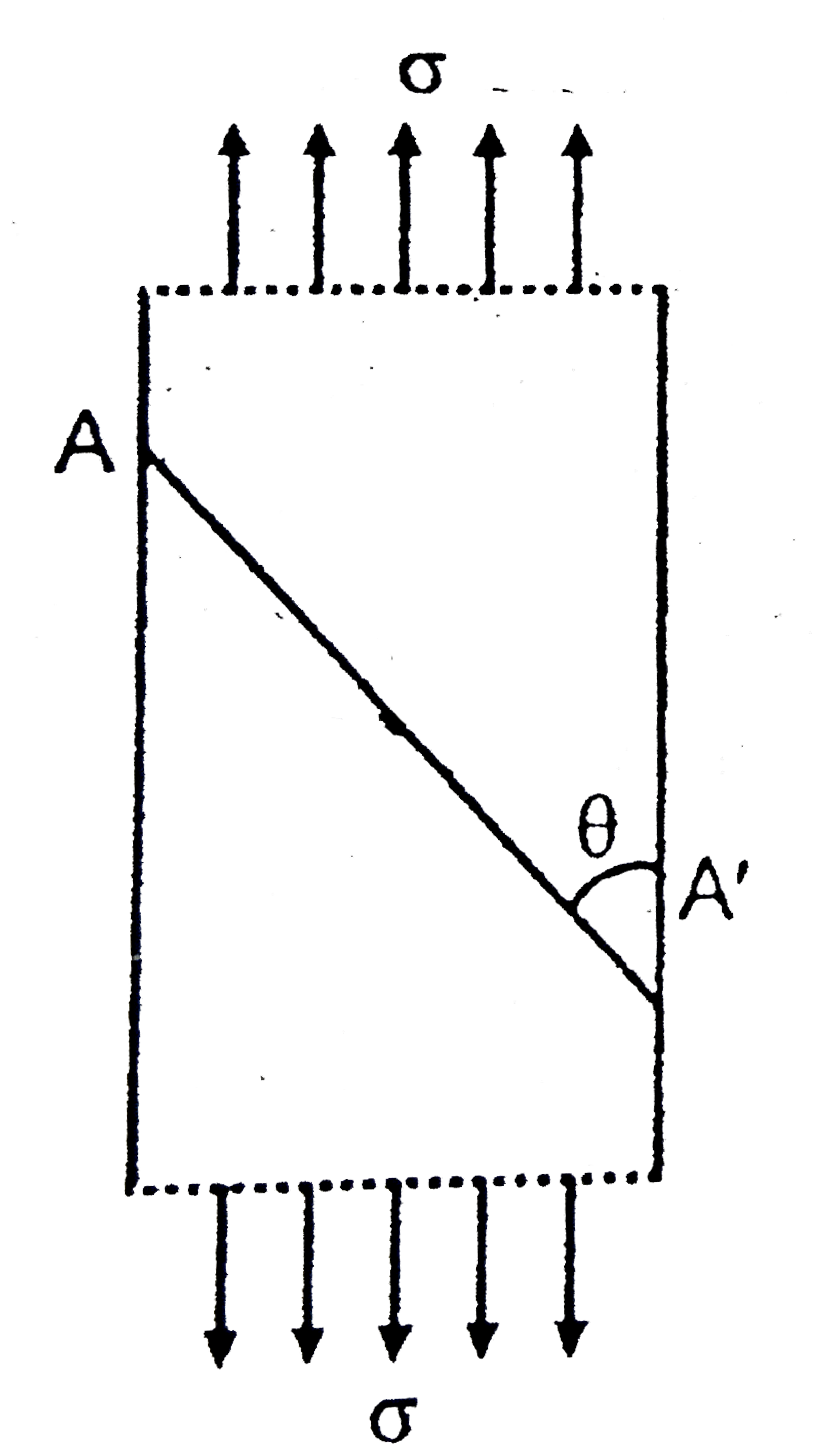
View SolutionA rectangular bar is uniformly loaded axially with force per unit area shown. Shown is a section in the bar. Normal stress for the section is

View SolutionFig shows a bar of uniform cross section of area s . Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F . ABCD is a plane trough the bar and inclined at angle theta with the perpendicular to the length of the bar. Normal stress at the plane which is inclined with the plane perpendicular to the length of the bar is -
View SolutionFig shows a bar of uniform cross section of area s . Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F . ABCD is a plane trough the bar and inclined at angle theta with the perpendicular to the length of the bar. Shear stress on theplane which is inclined with the plane perpendicular to the length of the bar is
View SolutionA chain of mass m and length L is held vertical such that its lower end just touches the floor. It is released from rest. Find the force exerted by the chain on the table when upper end is about to hit the floor.
View SolutionA vertical hanging bar of length and mass per unit length carries a load of mass at lower end, its upper end is clamped to a rigid support.The tensile stress a distance from support is ( area of cross - section of bar)
View SolutionA vertical hanging bar of length l and mass m per unit length carries a load of mass M at lower end, its upper end is clamped to a rigid support.The tensile stress a distance x from support is ( A rarr area of cross - section of bar)
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle as shown, find
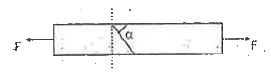
the shearing stress at this plane
View SolutionFig shows a bar of uniform cross section of area . Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude . ABCD is a plane trough the bar and inclined at angle with the perpendicular to the length of the bar.
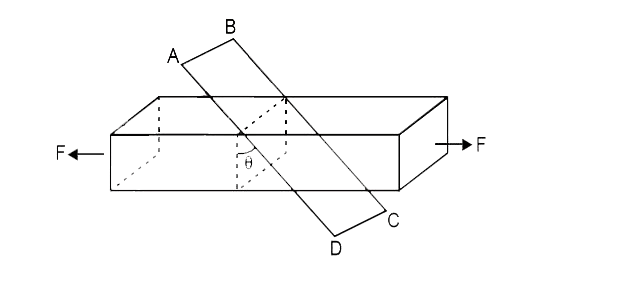
Shear stress on the inclined plane will be maximum for
View SolutionFig. shows a bar of uniform rectangular cross-section of area S. Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F. ABCD is a plane through the bar and inclined at angle phi with the plane perpendicular to the length of the bar. Shear stress on the said plane will be maximum for phi = :
View SolutionA uniformly tapering circular bar has its diameter ranging from (D-a) to (D+a) along its length L. The bar is subjected to an axial force P and young's modulus is Y. The percentage error in the calculation of elongation of bar if mean diameter is used in calculation instead of actual diameter.
View SolutionA uniformly tapering circular bar has its diameter ranging from (D-a) to (D+a) along its length L. The bar is subjected to an axial force P and young's modulus is Y. The percentage error in the calculation of elongation of bar if mean diameter is used in calculation instead of actual diameter.
View SolutionA metal bar of length L and area of cross-section A is rigidly champed between two walls. The Young's modulus of its material is Y and the coefficient of linear expansion is alpha . The bar is heated so that its temperature is increased by theta^(@)C . Find the force exerted at the ends of the bar.
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar as shown in figure.
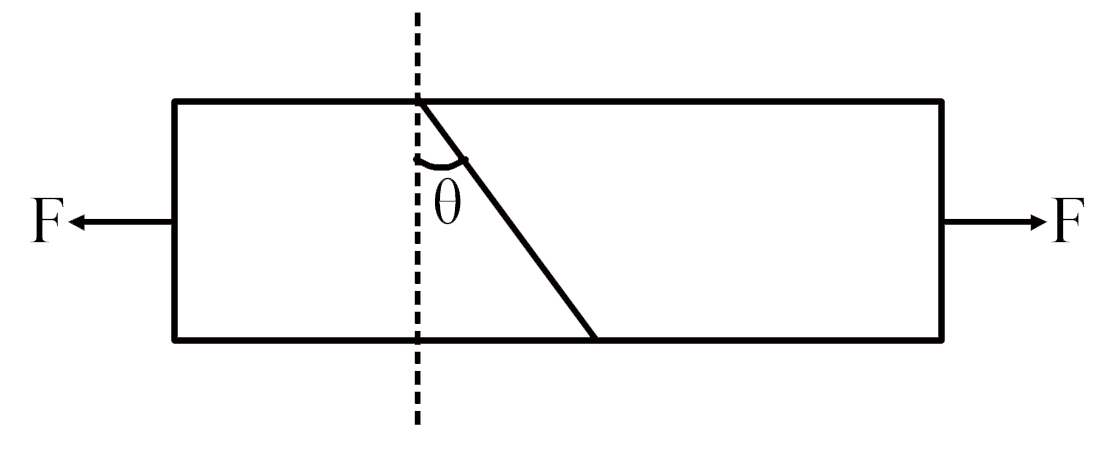
The tensile stress at this plane in terms of F, A and is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar as shown in figure.
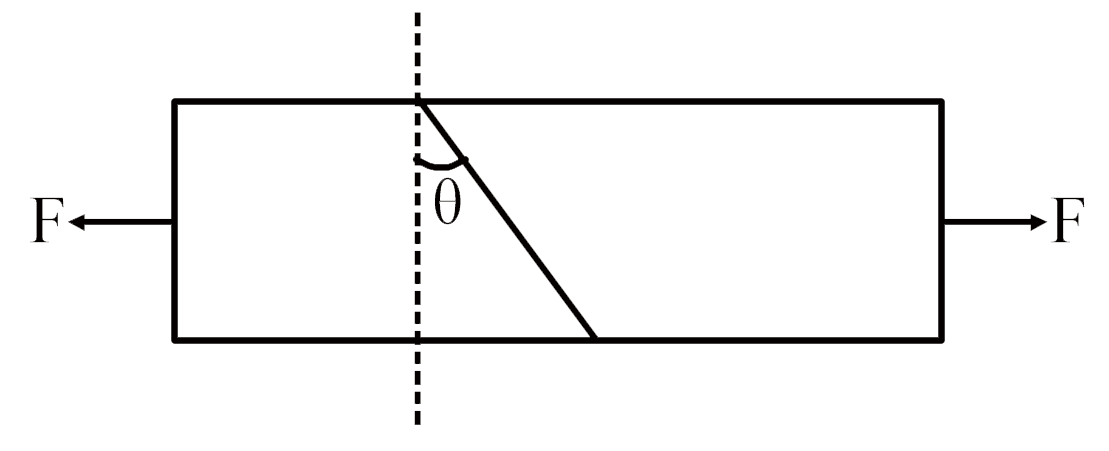
In the above problem, for what value of is the tensile stress maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle theta with a plane at right angles to the bar as shown in figure. The shearing stress at the plane, in terms of F, A and theta is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar as shown in figure.

The tensile stress at this plane in terms of F, A and is
View Solution