Figure below shows a small mass connected to a string which is attached to a vertical post. If the ball is released when the string is horizontal as shown the magnitude of the total acceleration including radial and tangential of the mass as a function of the angle θ is -A g sinθ B g √3cos2 θ + 1C g cosθ D g √3sin2 θ + 1
The correct Answer is:Option
Correct Option :- D g√3sin2 θ + 1Explanation :-
Related Solutions
Figure below shows a small mass connected to a string, which is attached to a vertical post. If the ball is released when the string is horizontal as shown, the magnitude of the total acceleration (including radial and tangential) of the mass as a function of the angle Theta is
View SolutionFor an acute angle θ, sinθ+cosθ takes the greatest value when θ is
View SolutionThe given figure shows a small mass connected to a string which is atteched to a string , which is attached to a vertical post. If the mass is released from rest when the string is horizontal as shown the magnitude of the total acceleration of the mass as friction of the angle theta is
View SolutionIf the determinant ∣ cos(θ+ϕ) sinθ −cosθ −sin(θ+ϕ) cosθ sinθ cos2ϕ sinϕ cosϕ ∣ is positive is independent of theta is independent of varphi none of these
View Solutionthen prove that
View Solution
Find
View SolutionFor the reaction,
and
Calculate for the reaction, and predict whether the reaction may occur spontaneously.
View SolutionFor the reaction, 2A(g)+B(g) rarr 2D(g) DeltaU^(Θ)=-10.5 kJ and DeltaS^(Θ)=-44.1 JK^(-1) Calculate DeltaG^(Θ) for the reaction, and predict whether the reaction may occur spontaneously.
View Solutionis equal to
(a)secθ+tanθ
(b) secθ−tanθ
(c) sec 2 θ+ tan 2 θ
(d) sec 2 θ− tan 2 θ
View SolutionIf sinΘ+cosec Θ=2 find the value of cotΘ+cosΘ
View SolutionIf ((sinθ−cosecθ)(cosθ−secθ))/(tan^(2)θ -sin^(2)θ) = r^3 , then r=? यदि ((sinθ−cosecθ)(cosθ−secθ))/(tan^(2)θ -sin^(2)θ) = r^3 है तो r बराबर हैः
View Solution(1 + cot2 θ) (1 – cos θ) (1 + cos θ) = …………………. (a) tan2 θ – sec2 θ (b) sin2 θ – cos2 θ (c) sec2 θ – tan2 θ (d) cos2 θ – sin2 θ
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m//s^2 )
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m//s^2 )
View SolutionIf is an acute angle and , find the value of .
View SolutionIf sinθ+sin^(2) θ=1, then prove that cos^(2)θ+cos^(4)θ =1
View SolutionTwo masses =5kg, =10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
(a) g (b) (c) (d)
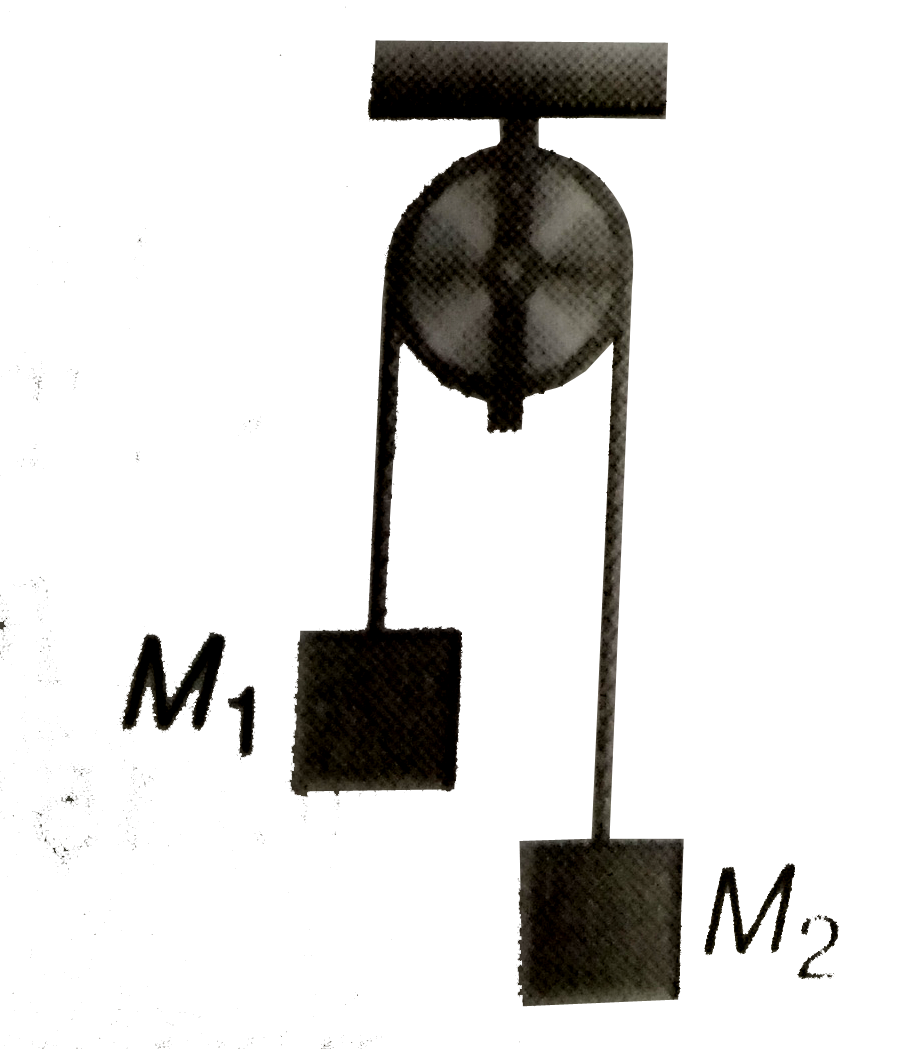
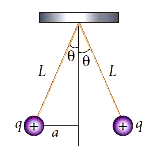
View SolutionTwo small-sized identical equally charged spheres, each having mass 1 mg are hanging in equilibrium as shown in the figure. The length of each string is 10 cm and the angle θ is 7° with the vertical. Calculate the magnitude of the charge in each sphere.
(Take )
View SolutionConsider the following changes : M_((s)) toM_((g)) " " ……..(1) M_((s)) +M_((g))^(2+) +2e^("ϴ")" "……..(2) M_((g)) to M_((g))^(+) +e^("ϴ") " "………(3) M_((g))^(+) to M_((g))^(+2) +e^("ϴ") " ".........(4) M_((g)) to M_((g))^(2+) +2e^("ϴ")" ".........(5) The second ionization energy of M_((g)) could be calculated from the energy values associated with :
View SolutionIn the figure shown acceleration with which the mass m falls down when released is ( consider the string to be massless g-acceleration due to gravity )
View Solution