all the seven questions1. The resultant of scalar product and vector product of two given vectors is zero. if one vector is i. What is the other vector?2. If A B C are any three vectors show that AxB+C = AxB +AxC3. A body is in equillibrium under the action of three vectors A B and C simultaneously. Show that AxB = BxC = CxA4. Express the magnitude of axb in terms of scalar products5. Find a.b and axb if a = i+2j+k and |b| = 3acting along c = i+j+k6. Prove that the vector area of triangle whose vertices are a b c is 1/2bxc + cxa + axb
Answer:1 If two vectors are collinear i.e. angle between them is 0 their vector product is 0. If two vectors are orthogonal i.e. angle between them is pi/2 their scalar product is 0. Thus if one vector is i the other one can be j k or any linear combination of j and k.2 Suppose r = A X B+C-AXB-AXC----iNow the scalar product of both sides with an arbitrary vector d d.r = d.[A X B+C-AXB-AXC]=d.[A X B+C]-d.AXB-d.AXC---iiSince scalar product is distributiveNow in a scalar triple product the positions of dot and cross can be interchanged without affecting its value.Therefore from ii we getd.r=dXA.B+C-dXA.B-dXA.C=dXA.B+dXA.C-dXA.B-dXA.C=0So Either d=0 or r=0 or d is perpendicular to r.But the vector d is arbitrary.So d=0 orAXB+C-AXB-AXC=0i.e AXB+C=AXB+AXC3 If the body is at equilibrium due to the 2nd Newtons Law A + B + C = 0. By multiplying it in sense of vector product by A from theleft we get AxA + AxB + AxC = 0. Some known rules: 1 Any vector product of collinear vectors is 0 so AxA =BxB = CxC = 0. 2 Changing the order of multipliers in the productchanges the sign: AxB = - BxA. Thus we have already AxB = - AxC = CxA. [i]By multiplying the original equation in the same fashion byB we get BxA + BxC = 0; AxB = - BxA = BxC. [ii]Results [i] and [ii] provide enough evidence to say that A X B = B X C = CXA.4 If a and b are vectors and aXb is their vector product the magnitude of it is absaXb = absa*absb*sina b where a b is the angle between the vectors a and b. If a.b is the scalar product of these two vectors it is a.b= absa*absb*cosa b and the magnitude of the vector product is absaXb = a.b * sina b / cosa b = a.b*tana b.
Related Solutions
The result of scalar product and the vector product of two given vectors is zero . If one vector is hat(i) what is the other vector ?
View SolutionLet a and b be given non-zero and non-collinear vectors, such that . Express c in terms for a, b and aXb.
View SolutionLet a and b be given non-zero and non-collinear vectors, such that . Express c in terms for a, b and aXb.
View SolutionLet a and b be given non-zero and non-collinear vectors, such that . Express c in terms for a, b and aXb.
View SolutionThe scalar triple product of vectors is zero if______a)One of the vectors is zero vectors b)Any two vectors are non-collinear c)Three vectors are non-coplanar d)All of the above
View SolutionCross Product Of Vectors|Right Hand Thumb Rule|Properties Of Cross Product|Method For Cross Product|Questions|Unit Vector Perpendicular To A & B (In AxB )
View SolutionDefine scalar product of two vectors . Show of two vectors . Show that scalar product of vectors satisfies the commutative and distributive laws.
View SolutionIf a,b and c are three non-coplanar vectors, then the scalar product of vectors and is
View SolutionIf are three mutually perpendicular vectors of equal magnitude, then the angle which makes with any one of three given vectors, is given by
View SolutionIf a,b and c are three mutually perpendicular vectors of equal magnitude then the angle which a + b + c makes with any one of three given vectors is given by
View SolutionShow that the magnitude of a vector is equal to the square root of the scalar product of the vector with itself .
View Solutionকোনোটাই শূন্য ভেক্টর নয় এমন তিনটি ভেক্টর , , -এর যে-কোনো দুটি সমরেখ নয়। যদি ভেক্টর ভেক্টরের সঙ্গে সমরেখ হয় এবং ভেক্টর ভেক্টরের সঙ্গে সমরেখ হয়, তবে প্রমাণ করো যে, একটি শূন্য ভেক্টর।
View Solutionप्रककथनः यदि सदिशों तथा का अदिश तथा सदिश दोनों गुणनफल शून्य है इसका अर्थ है कि तथा में से कोई एक सदिश शून्य है।
कारणः शून्य सदिश वह सदिश है जिसका परिमाण शून्य होता हैं
View Solution[abc] is the scalar triple product of three vectors a, b and c then [abc] is equal to
View Solution[abc] is the scalar triple product of three vectors, a, b, and c then [abc] is equal to
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
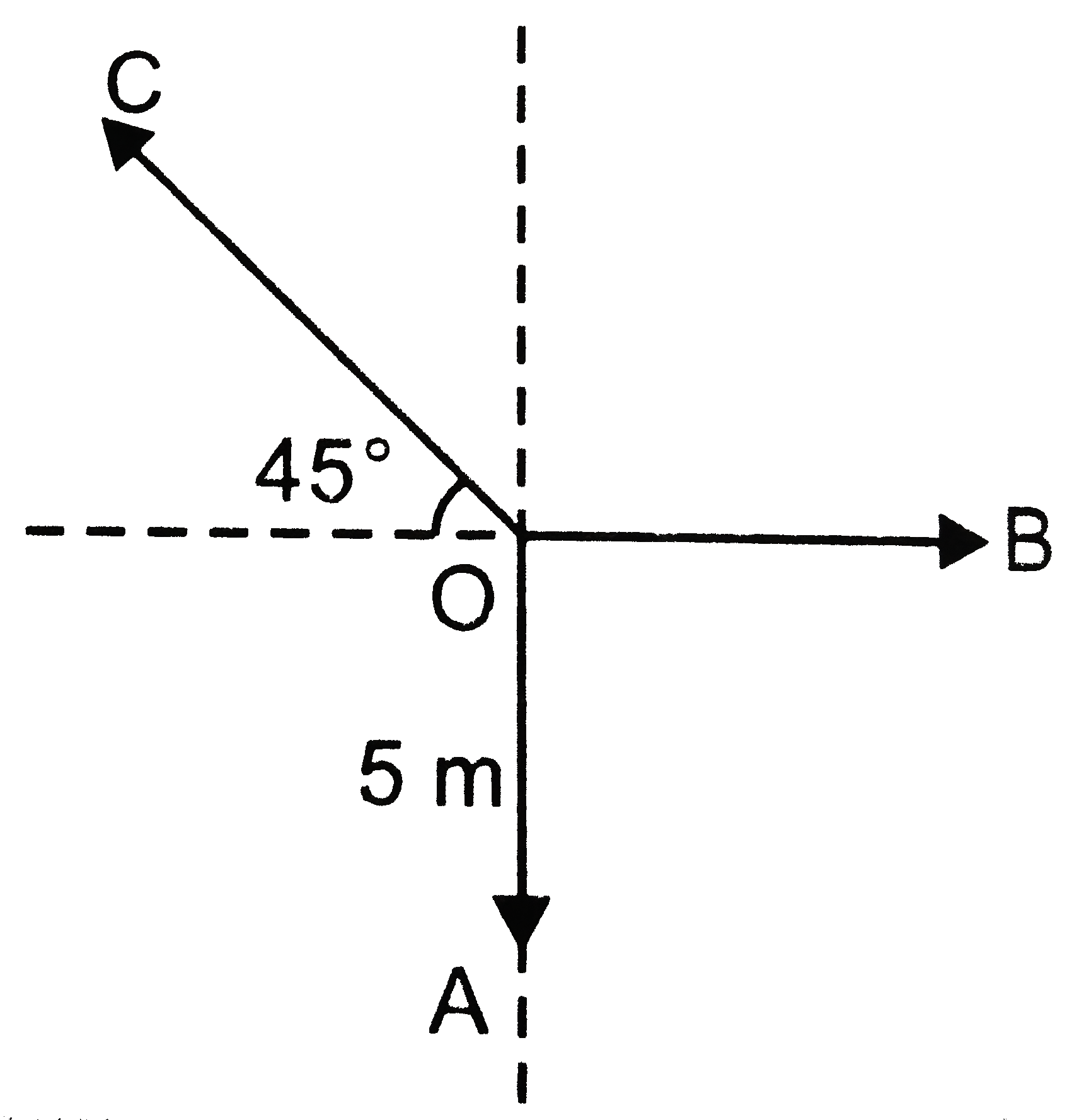 .
.
(a) What is the magnitude of the vector ?
(b) What is the magnitude of the vector ?
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
 .
.
(a) What is the magnitude of the vector ?
(b) What is the magnitude of the vector ?
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
 .
.
(a) What is the magnitude of the vector vec (OC) ?
View SolutionCan the resultant be zero in case of : (a) two unequal vectros (b) three coplanar vectors (c) three non- complanar vectors
View SolutionAssertion: The scalar product of two vectors can be zero Reason: If two vectors are perpendicular to each other their scalar product will be zero.
View Solution