The large container shown in the cross section is filled with a liquid of density 1.1 x 103 kg/m3. hole of area 2.5 x 10-6m2. A small is opened in the side of the container a distance h below the liquid surface which allows a stream of liquid to flow through the hole and into a beaker placed to the right of the container. At the same time liquid is also added to the container at an appropriate rate so that h remains constant. The amount of liquid collected in the beaker in 2.0 minutes is 7.2 x 10–4m3.a Calculate the volume rate of flow of liquid from the hole in m3s.b Calculate the speed of the liquid as it exits from the hole. c Calculate the height h of liquid needed above the hole to cause the speed you determined in part b. d Suppose that there is now less liquid in the container so that the height h is reduced to h/2. In relation to the collection beaker where will the liquid hit the tabletop? ____ Left of the beaker ____ In the beaker ____ Right of the beaker
a Volume flow rate = Q = V/t = 7.2 x 10–4/2min * 60 sec/min = 6 x 10–6m3/s b Your first thought is probably Bernoulli but there are too many unknowns so this does not work. We can use the volume flow rate above the find the velocity. Q = Av 6 x 10–6 = 2.5 x 10–6v v = 2.4 m/s c Use Bernoulli … v2 = √2gh 2.4 = √29.8h h=0.29m d Left of beaker. Based on the formula derived above the exit velocity is dependent on the height and with less horizontal exit velocity the range will be less dx = vxt. This makes sense because less height would result in less pressure and decrease the speed the fluid is ejected at thus lessening the range.
Related Solutions
A liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
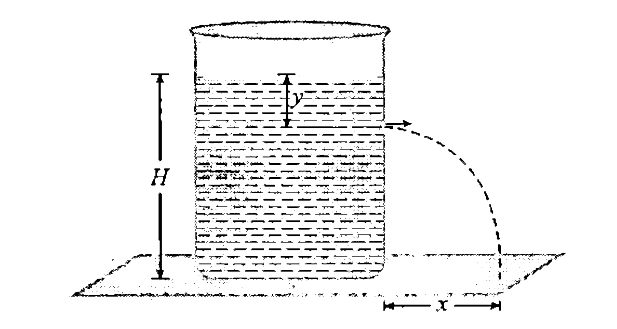
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
View SolutionA cylindrical vessel contains a liquid of density up to height . The liquid is closed by a piston of mass and area of cross section . There is a small hole at the bottom of the vessel. The speed with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density rho up to height h . The liquid is closed by a piston of mass m and area of cross section A . There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
View SolutionA cylindrical vessel contains a liquid of density rho up to height h . The liquid is closed by a piston of mass m and area of cross section A . There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
View SolutionThere is a small hole in the bottom of a fixed container containing a liquid upto height . The top of the liquid as well as the hole at the bottom are exposed to atmosphere. As the liquid come out of the hole. (Area of the hole is and that of the top surface is ) :
View SolutionThere is a small hole in the bottom of a fixed container containing a liquid upto height . The top of the liquid as well as the hole at the bottom are exposed to atmosphere. As the liquid come out of the hole. (Area of the hole is and that of the top surface is ) :
View SolutionA cylindrical vessel contains a liquid of density up to height . The liquid is closed by a piston of mass and area of cross section . There is a small hole at the bottom of the vessel. The speed with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density rho upto a heighth The liquid is closed by a piston of mass m and area of cross-section A. There is a small hole at the bottom of the vessel. Find the speed with which the liquid comes out of the hole
View SolutionA cylindrical vessel contains a liquid of density upto a heighth The liquid is closed by a piston of mass m and area of cross-section A. There is a small hole at the bottom of the vessel. Find the speed with which the liquid comes out of the hole
View SolutionA liquid of density is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionA liquid of density rho is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionA hole is made at a depth h on the wall of a container containing a liquid. The velocity of efflux of the liquid through the hole is
View SolutionA large container contains a liquid of density p, mass m, and placed on a smooth horizontal floor. The mass of container is negligible and cross sectional area is A. Now at the bottom of the container, there is small hole of cross section area A/200 in the side wall through which the liquid starts flowing horizontally at t=0. What will be the velocity of efflux when half of the liquid is drained out. Also, find the acceleration of the liquid flowing out.
View SolutionA large container (with open top) of negligible mass and uniform cross-sectional area A has a small hole of cross-sectional area a in its side wall near the bottom. The container contains a liquid of density rho and mass m. If the liquid starts flowing out of the hole at time t = 0, the velocity of efflux of the liquid when 75% of the liquid has drained out is:
View SolutionCalculate the velocity with which a liquid emerges from a small hole in the side of a tank of large cross-sectional area if the hole is 0.2 m below the surface liquid (g = 10 "ms"^(-2) .
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
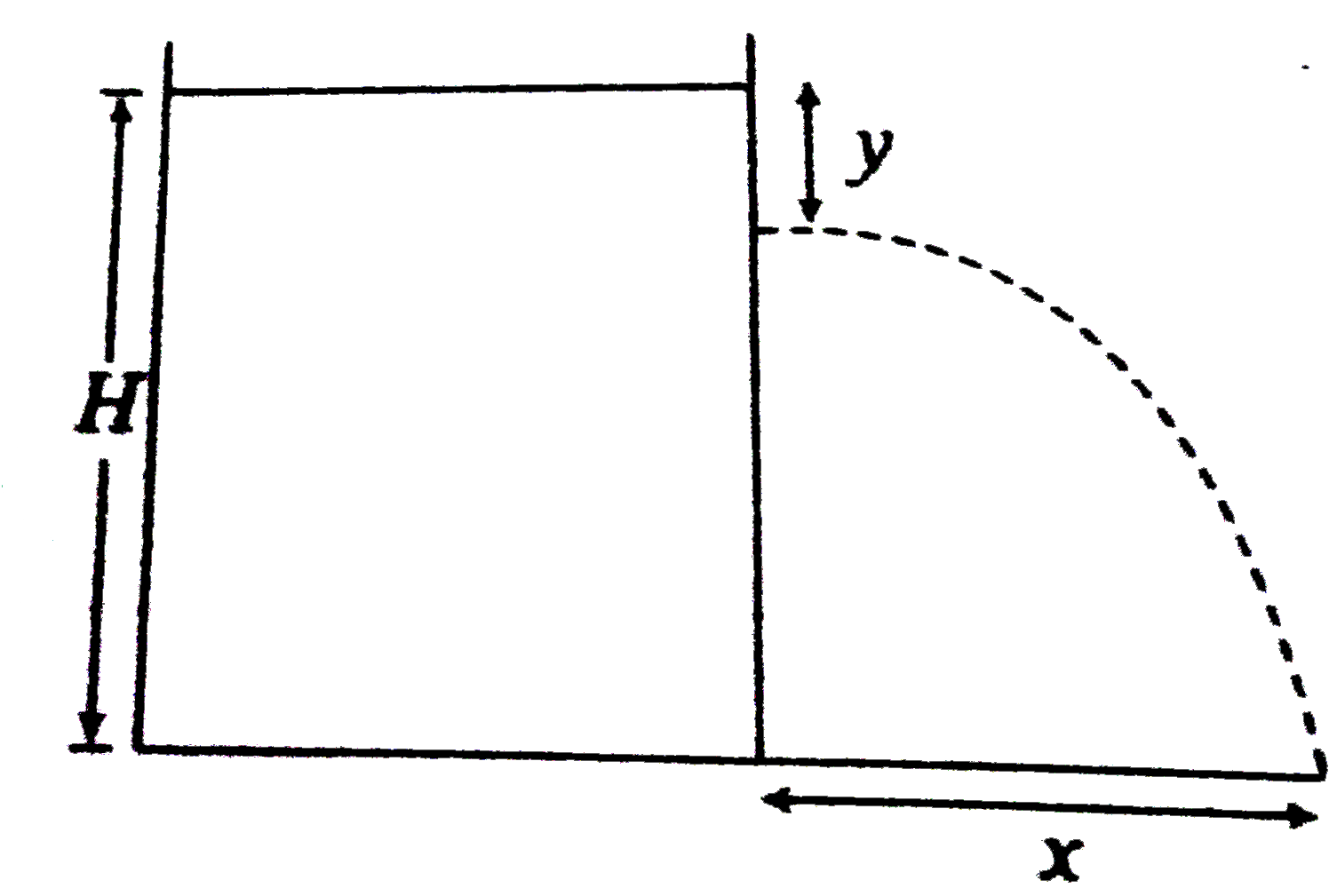
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
View SolutionA large open top container of negligible mass and uniform cross sectional area a has a small hole of cross sectional area in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density and mass . Assuming that the liquid starts flowing out horizontally through the hole at , calculate a the acceleration of the container and its velocity when of the liquid has drained out.
View Solution