Two stars A and B. are in circular orbits of radii ra and rb respectively about their common enter of mass at point P as shown. Each star has the same period of revolution T.Determine expressions for the following three quantities in terms of ra rb T and fundamental constants.a. The centripetal acceleration of star Ab. The mass Mb of of star Bc. The mass Ma of star Ad. Determine an expressions for the angular momentum of the system about the center of mass in terms of Ma Mb ra rb T and fundamental constants.
c. The same calculations can be performed with the roles of star A and star B switched.
Related Solutions
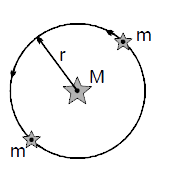
A certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionAn isolated triple star systerm consists of two identical stars, each of mass and f fixed star of mass . They revolve around the central star in the same circular orbit to radius . The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:

View SolutionAn isolated triple star systerm consists of two identical stars, each of mass m and f fixed star of mass M . They revolve around the central star in the same circular orbit to radius r . The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:
View SolutionA star of mass M (equal to the solar mass) with a planet (much smaller than the star) revolves around the star in a circular orbit. The velocity of the star with respect to the center of mass of the star-planet system is shown below :
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other has mass m such that =2m. The distance between the centres of the stars is d ( d being large compare to the size of eithe star).
The period of rotation of the stars about their common centre of mass ( in terms of d,m,G) is
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass and the other has mass m such that The distance between the centres of the stars is d (d being large compared to the size of either star) .
The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionTwo identical stars of mass M orbit around their centre of mass. Each orbit is circular and has radius R, so that the two stars are always on opposite sides of the circle.
The orbital speed of the each star in the orbit is
View Solution_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass . The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is m and the orbital period each star is [take and ]
Q. The mass m of the outer stars is:
View Solution_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass . The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is m and the orbital period each star is [take and ]
Q. The mass m of the outer stars is:
View Solution_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass . The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is m and the orbital period each star is [take and ]
Q. The mass m of the outer stars is:
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other m . Their centres are a distance d apart, d being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies.
View SolutionA triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2xx10^(33)kg . The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=10^(11) m and the orbital period each star is 1.6xx10^(7)s [take pi^(2)=10 and G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2) ] Q. The orbital velocity of each star is
View SolutionA triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2xx10^(33)kg . The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=10^(11) m and the orbital period each star is 1.6xx10^(7)s [take pi^(2)=10 and G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2) ] Q. The orbital velocity of each star is
View SolutionA triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2xx10^(33)kg . The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=10^(11) m and the orbital period each star is 1.6xx10^(7)s [take pi^(2)=10 and G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2) ] Q. The orbital velocity of each star is
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about a centre of mass midways between them. Orbital speed of each star is v & period of revolution is T. Find the mass M of each star. (G is gravitational constant )
View SolutionA triple star system consists of two stars each of mass m in the same circular orbit about central star with mass M=2xx10^(33)kg . The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=10^(11) m and the orbital period each star is 1.6xx10^(7)s [take pi^(2)=10 and G=(20)/(3)xx10^(-11)Mn^(2)kg^(-2) ] Q. The orbital velocity of the outer stars is:
View Solution