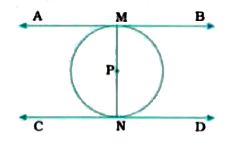
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:Let AB be a diameter of the circle. Two tangents PQ and RS are drawn at points A and B respectively.Radii of the circle to the tangents will be perpendicular to it.∴ OB ⊥ RS and ∴ OA ⊥ PQ∠OBR = ∠OBS = ∠OAP = ∠OAQ = 90ºFrom the figure ∠OBR = ∠OAQ Alternate interior angles∠OBS = ∠OAP Alternate interior anglesSince alternate interior angles are equal lines PQ and RS will be parallel.Hence Proved that the tangents drawn at the ends of a diameter of a circle are parallel.
Related Solutions
Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter fo a circle are parallel .
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View Solutionਸਿੱਧ ਕਰੋ ਕਿ ਕਿਸੇ ਚੱਕਰ ਦੇ ਕਿਸੇ ਵਿਆਸ ਦੇ ਸਿਰਿਆਂ 'ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਸਮਾਂਤਰ ਹੁੰਦੀਆਂ ਹਨ।
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the ends of a diameter of a circle are parallel.
View SolutionProve that tangent drawn at the ends of a diameter of a circle are parallel.
View Solutionसिद्ध कीजिए कि वृत्त के व्यास के छोर पर खींची गई स्पर्श रेखाएँ समान्तर होती है।
View SolutionProve that the tangents drawn at the ends of a diameter fo a circle are parallel .
View Solutionಒಂದು ವೃತ್ತಕ್ಕೆ ವ್ಯಾಸದ ಅಂತ್ಯಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳು ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿವೆ ಎಂದು ಸಾಧಿಸಿ.
View SolutionProve that the tangents drawn to a circle at the two ends of a diameter are parallel.
View Solutionसिद्ध करें की किसी वृत्त के किसी व्यास के सिरों पर से खींची गई स्पर्श रेखाएँ समांतर होती हैं|
View Solutionसिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं ।
View Solutionसिद्ध कीजिए कि एक वृत्त के व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर समांतर होती हैं।
View Solution