A 50° B 60° C 70° D 80°
Solution:OA and OB are radii of the circle to the tangents PA and PB respectively.∴ OA ⊥ PA and ∴ OB ⊥ PB∠OBP = ∠OAP = 90°In quadrilateral AOBP Sum of all interior angles = 360°∠AOB + ∠OBP + ∠OAP + ∠APB = 360°⇒ ∠AOB + 90° + 90° + 80° = 360°⇒ ∠AOB = 100°Now In ΔOPB and ΔOPA AP = BP Tangents from a point are equalOA = OB Radii of the circleOP = OP Common side∴ ΔOPB ≅ ΔOPA by SSS congruence conditionThus ∠POB = ∠POA∠AOB = ∠POB + ∠POA⇒ 2 ∠POA = ∠AOB⇒ ∠POA = 100°/2 = 50°∠POA is equal to option A 50°
Related Solutions
In Figure, the measure of is
(a)
(b)
(c)
(d)
View SolutionIn Figure, the measure of is
(a)
(b)
(c)
(d)
View Solution70, 80, 50, 60, 70, 40, 50, 90, 50, 30 का बहुलक होगा
View Solutionनिम्नलिखित आँकड़ों का बहुलक ज्ञाता कीजिए।
50, 70, 50, 70, 80, 70, 70, 80, 70, 50.
View SolutionIf the sum of a number and its two-fifth is 70. The number is
(a)70 (b) 50 (c)60 (d) 90
View Solution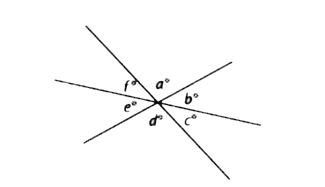
If and d = 80 what is b?
View SolutionIf U = {10, 20, 30, 40, 50, 60, 70, 80, 90} universal set. and A = {10, 20, 40, 60} B = {30, 40, 60, 80} C = {10, 30, 60, 90} find (A')'
View SolutionIf U = {10, 20, 30, 40, 50, 60, 70, 80, 90} universal set. and A = {10, 20, 40, 60} B = {30, 40, 60, 80} C = {10, 30, 60, 90} find A'
View SolutionIf a liquid takes seconds in cooling of to and seconds in cooling to , then find the room temperature.
View SolutionIf a liquid takes seconds in cooling of to and seconds in cooling to , then find the room temperature.
View SolutionIf a liquid takes seconds in cooling of to and seconds in cooling to , then find the room temperature.
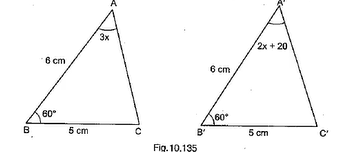
View SolutionIf and are similar triangles such that and , then (a) (b) (c) (d)
View Solution30, 80, 60, 70, 20, 40, 50 இவற்றின் திட்டவிலக்கம் காண்க ?
View Solutionऔर मे यदि , और हो तो
View Solutionas a fraction is (a) (b) (c) (d)
View Solutionas a fraction is
(a)
(b)
(c)
(d)
View Solutionकक्षा X के 30 विद्यार्थियों की वार्षिक बचत (रुपयों में) नीचे दी गई हैं :
50, 53, 70, 70, 80, 60, 53, 75, 47, 47
47, 75, 53, 60, 70, 70, 80, 53, 50, 53
70, 75, 75, 60, 80, 80, 47, 50, 50, 50.
मिलान चिह्नों का प्रयोग करते हुए सारणी बनाइए।
अधिकतम बचत कितनी है ?
View Solutionकक्षा th के विद्यार्थियों की वार्षिक बचत (रुपयों में) नीचे दी गई हैं :
मिलान चिह्नों का प्रयोग करते हुए सारणी की सहायता से बताइए कि न्यूनतम बचत कितनी है ?
View SolutionCalculate the mean, variance and standard deviation for the following distribution :
View SolutionIf the sum of a number and its two-fifth is 70. The number is 70 (b) 50 60 (d) 90
View Solution
