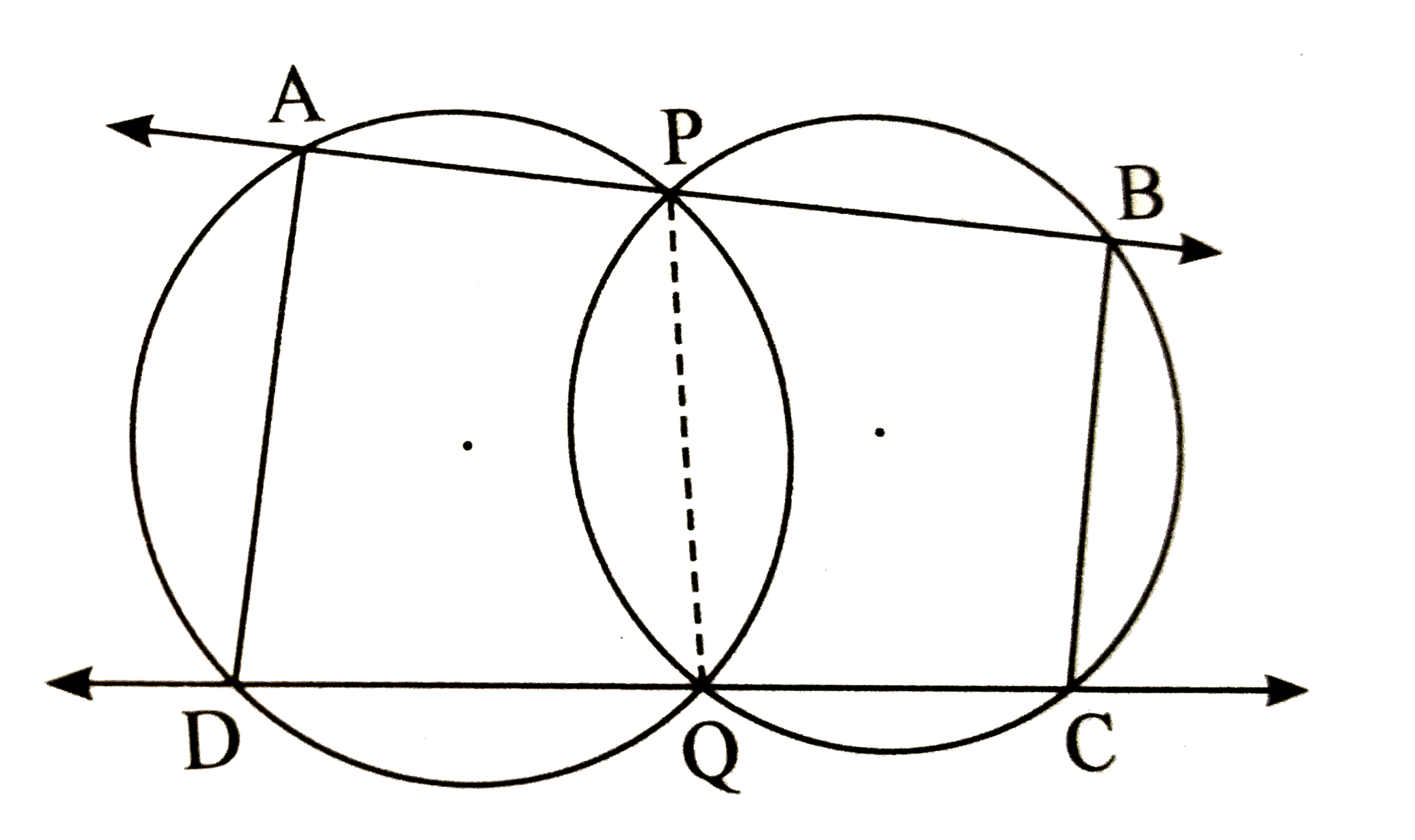
Two circles intersect each other at points P and Q. Secants drawn through P and Q intersect the circles at points A B and D C.Prove that : ∠ADC + ∠BCD = 180o
Draw Seg PQ. APQD is a cyclic qudrilateral. ∠ ADQ + ∠ APQ = 180o ....... 1PBCQ is a cyclic qudrilateral. ∴ ∠ BCQ + ∠ BPQ = 180o ...... 2∴ ∠ ADQ + ∠ APQ + ∠ BCQ + ∠ BPQ = 180o +180o .... [from 1 2 ] ∴ ∠ ADQ + ∠ BCQ + ∠ APQ + ∠ BPQ = 180o + 180o ...... 3But∠ APQ + ∠ BPQ = 180o ............ 4 angles in linear pair ∴ ∠ ADQ + ∠ BCQ + 180o = 180o + 180o ............ [from 3 4 ] ∴ ∠ ADQ + ∠ BCQ = 180o ∴ ∠ ADC + ∠ BCD = 180o
Related Solutions
Two circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and
the other circle at B and D. Prove the AC|| BD
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionTwo circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that
View SolutionTwo congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that .
View SolutionIn the adjoining figure, two circles intersect each other at points M and N . Secants drawn from points M and N intersect cirecls at point R, S, P and Q as shown in the figure.
View SolutionA and B are the points where the two circles in the figure intersect. P and Q are the other ends of the diameters through A. Prove that the points P, B and Q are on the same line.
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that seg SQ seg RP.

View SolutionIn the adjoining figure ,two circles intersect at points M and N. |
Secants drawn through M and N intersect the circles at points R,S
and P,Q respectively. Prove that: seg SQseg RP.
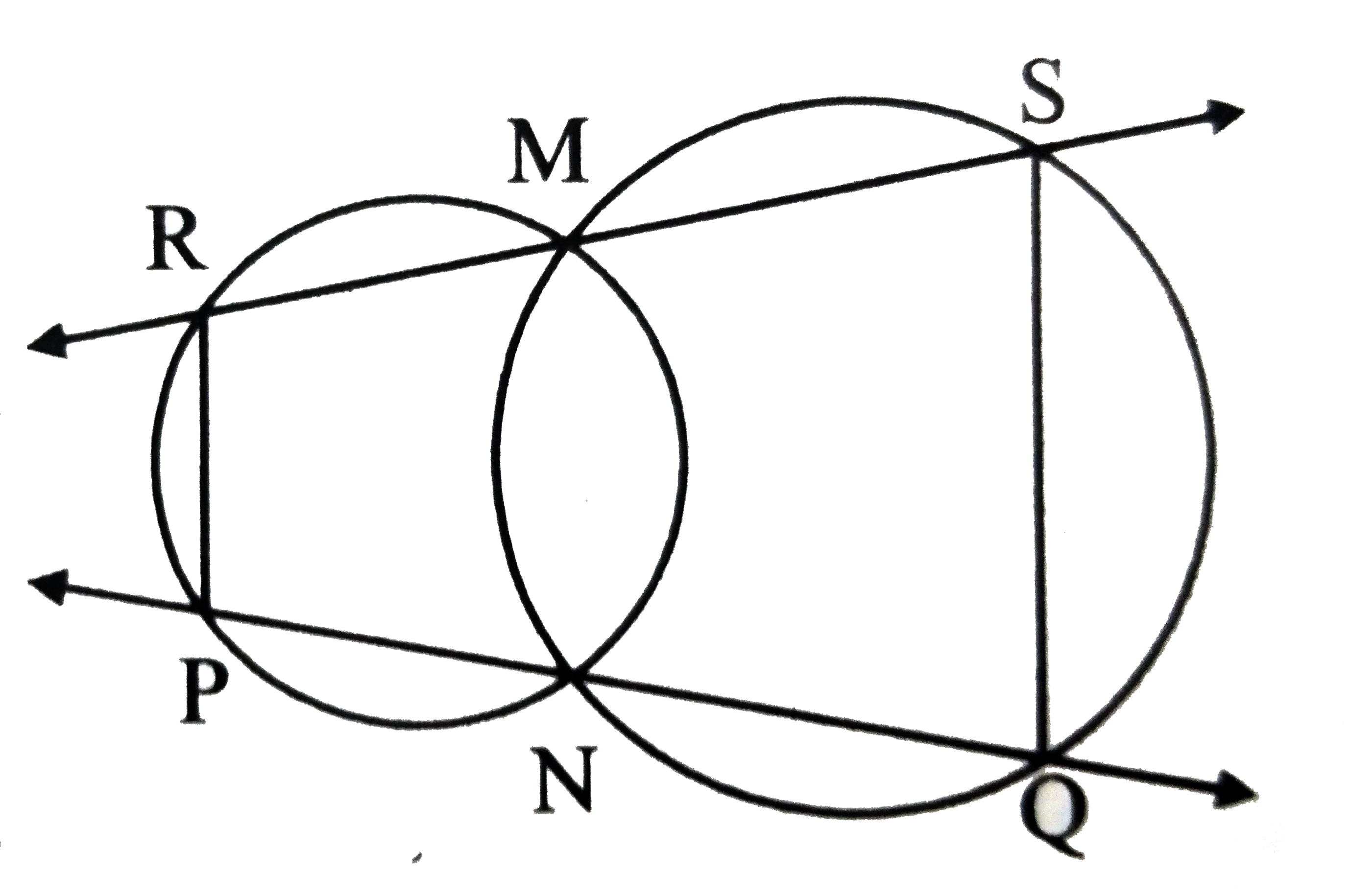
View SolutionIn figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ || seg RP.

View SolutionTwo circles intersect each other at the points P and Q. A straight line passing through P intersects one circle at A the other circle at .A straight line passing through Q intersect the first circle at C and the second circle at D. Prove that .
View Solutionदो समान वृत्त एक-दूसरे को बिन्दुओं A और B पर काटते हैं | A से होकर जाने वाली एक वृत्तों को P और Q बिन्दुओं पर मिलती है | सिद्ध कीजिए कि BP = BQ.
View Solutionदो वृत्त एक दूसरे को P,Q बिन्दुओ पर प्रतिछेदित करती है। एक छेदक रेखा जो P बिंदु से गुजरती है वह वृतो को क्रमश A और B बिंदु पर प्रतिछेद करती आहे तथा A और B पर खींची गयी स्पर्श रेखाएं T बिंदु पर मिलती है तो सिद्ध कीजिये की A,Q,B और T एक वृतीय है
View SolutionTwo cirlces intersect at P and Q . Through P diameter PA and PB of the two circles are drawn. Show that the points A,Q and B are collinear.
View SolutionTwo circles intersect each other at the points G and H . A straight line is drawn through the point G which intersect two circles at the points P and Q and the straight line through the point H parallel to PQ intersects the two circles at the points R and S . Prove that PQ=RS .
View SolutionTwo circles intersect each other at points P and Q. From point P, diameters PA and PB are drawn on both the circles. Show that A, Q and B are collinear
View SolutionA line which intersect the circle at two points (P and Q) is called a.................. of the circle.
View Solution