Two stars of masses m1 and m2 distance r apart revolve about their centre of mass. The period of revolution is
Correct option dExplanation:Let the distances of the stars with masses m1 and m2 from their centre of mass be r1 and r2 respectively so that r1 + r2 = r say. The necessary centripetal force is provided by the gravitational force between them so that G m1m2/r2 = m1r1ω2 = m2r2ω2.This gives ω2 = Gm2/r2r1 =Gm1/r2r2 = Gm1+m2/r2r1 + r2 = Gm1+m2/r3 From this one can write the expression for T.
Related Solutions
Two stars of masses and distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo stars of masses and distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo stars of masses m_(1) and m_(2) distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is :
View SolutionIn a double star, two stars one of mass and another of mass , with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.
View SolutionIn a certain binary star system, each star has the same mass as our sun. They revolve about their centre of mass. The distance between them is the same as the distance between earth and the sun. What is their period of revolution in years ?
View SolutionIn a certain binary star system, each star has the same mass as our sun. They revolve about their centre of mass. The distance between them is the same as the distance between earth and the sun. What is their period of revolution in years ?
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other m . Their centres are a distance d apart, d being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies.
View SolutionIn a double star, two stars (one of mass and the other of mass ) distance apart rotate about their common centre of mass., Deduce an expressioin for the period of revolution. Show that te ratio of their angular momenta about the centre of mass is the same as the ratio of their kinetic energies.
View SolutionTwo stars of masses m and 2m are co-rotating about their centre of mass. Their centres are at a distance r apart. If r is much larger than the size of stars then, their kinetic energies are in the ratio x : y. The value of xy is
View SolutionIn a certain binary-star system, each star has the same mass as our Sun, and they revolve about their center of mass. The distance between them is the same as the distance between Earth and the Sun. What is their period of revolution in years ?
View SolutionA double star is a system of two stars of masses m and 2 m, revolving about their centre of mass only under their mutual gravitational attraction. If r is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionIn a double star system, two stars of masses m_1 and m_2 separated by a distance x rotate about their centre of mass. Find the common angular velocity and Time period of revolution.
View SolutionIn a double star system two stars of masses separated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionIn a double star system two stars of masses and seperated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionTwo stars of a binary system are separated by a distance of 20 AU with a period of revolution of 20 years. One of the two stars is 4 times farthest from the centre of mass of the other. Find masses of each star.
View SolutionA certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
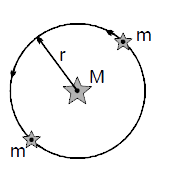
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about a centre of mass midways between them. Orbital speed of each star is v & period of revolution is T. Find the mass M of each star. (G is gravitational constant )
View Solution