In a Young’s Double slit experiment first maxima is observed at a fixed point P on the screen. Now the screen is continuously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O centre of the screen a remains constant b keeps on decreasing c first decreases and then increases d first decreases and then becomes constant
Correct option: c first decreases and then increasesExplanation: Initially phase difference is 2π with increasing distance of screen phase difference decreases to π and than to zero.
Related Solutions
In a young.s Double slit experiment ,first maxima is observed at a fixed point P on the screen Now the screen is continuously moved away from the plane of slits . The ratio of intensity at point P to the intensity at point O (centre of the screen )
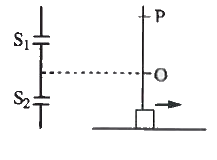
View SolutionIn Young's Double slit experiment, first maxima is observed at a fixed point P on the screen. Now the screen is continuously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (centre of the screen)
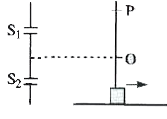
View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)

View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)
View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)
View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)
View SolutionIn Young's double slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is and d is the distance between the slits, the angular separation between point P and the centre of the screen is ......
View SolutionIn Young's double slit experiment, (d=distance between slits, D-distance of screen from the slits). At a point P on the screen resulting intensity is equal to the intensity due to individual slit . Then the distance of point P from the central maxima is (
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionFind the ratio of intensities at two points on a screen in young’s double slit experiment when waves from the two slits have path difference of .
View SolutionIn Young's double-slit experiment (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit . Then, the distance of point P from the central maximum is
View SolutionIn Young's double slit experiment (d)/(D) = 10^(-4) (d = distance between slits, D = distance of screen from the slits) At a point P on the screen the resulting intensity is equal to the intensity due to individual slit I_(0) .Then the distance of point P from the central maximum is (lambda = 6000 Å) :
View SolutionIn Young's double-slit experiment d//D = 10^(-4) (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit I_(0) . Then, the distance of point P from the central maximum is (lambda = 6000 Å)
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
View SolutionIn the Young’s double slit experiment, the resultant intensity at a point on the screen is 75% of the maximum intensity of the bright fringe. Then the phase difference between the two interfering rays at that point is
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen.
Find the value of n.
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. Find the value of n.
View SolutionIn a single-slit diffraction experiment, light of wavelength illuminates the slit of width 'a' and the diffraction pattern is observed on a screen.
(a) Show the intensity distribution in the pattern with the angular position .
(b) How are the intensity and angular width of central maxima affected when
(i) width of slit is increased, and
(ii) separation between slit and screen is decreased ?
View Solution