A non - conducting ring of mass m and radius R is charged as shown. The charged density i.e. charge per unit length is λ. It is then placed on a rough non - conducting horizontal surface plane. At time t=0 a uniform electric field E =E0i is switched on and the ring start rolling without sliding. Determine the frictional force magnitude and direction acting on the ring when it starts moving.
Friction acts in forward direction decreases angular acceleration and increasing linear acceleration2 is multiplied considering –ve changes also
Related Solutions
A nonconducting ring of mass m and radius R is charged as shown. The charged density i.e. charge per unit length is . It is then placed on a rough nonconducting horizontal surface plane. At time t = 0, a uniform electric field is switched on and the ring starts rolling without sliding. The friction force (magnitude and direction) acting on the ring, when it starts moving is
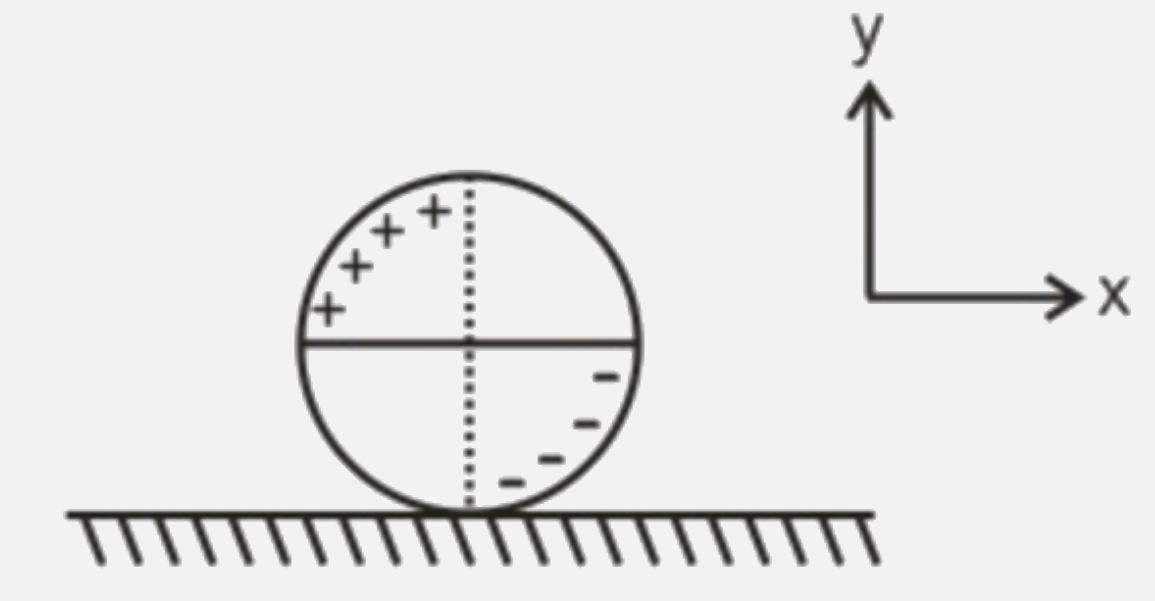
View SolutionA nonconducting ring of mass m and radius R, with charge per unit length lambda is shown in fig. It is then placed on a rough nonconducting horizontal plane. At time t=0, a uniform electric field vecE =E_(0)hati is switched on and the ring starts rolling without on and the ring starts rolling without sliding. Determine the friction froce (magnitude and direction ) acting on the ring.
View SolutionA nonconducting ring of mass m and radius R, with charge per unit length is shown in fig. It is then placed on a rough nonconducting horizontal plane. At time t=0, a uniform electric field is switched on and the ring starts rolling without sliding. Determine the friction force (magnitude and direction ) acting on the ring.

View SolutionA nonconducting ring of mass m and radius R, with charge per unit length lambda is shown in fig. It is then placed on a rough nonconducting horizontal plane. At time t=0, a uniform electric field vecE =E_(0)hati is switched on and the ring starts rolling without sliding. Determine the friction force (magnitude and direction ) acting on the ring.
View SolutionA non conducting ring of radius R is charged as shown in figure : Figure
View SolutionA non conducting solid sphere of mass m and radius R having uniform charge density +rho and -rho as shown in figure. It is then placed on a rough non conducting horizontal plane. At t=0 a uniform electric field vecE=E_(0)hati N//C is switched on and the solid sphere starts rolling with sliding. The magnitude of frictional force at t=0 is (2rhopiR^(3)E_(0))/K . Find the value of K
View SolutionA non conducting solid sphere of mass m and radius R having uniform charge density +rho and -rho as shown in figure. It is then placed on a rough non conducting horizontal plane. At t=0 a uniform electric field vecE=E_(0)hati N//C is switched on and the solid sphere starts rolling with sliding. The magnitude of frictional force at t=0 is (2rhopiR^(3)E_(0))/K . Find the value of K
View SolutionA non-conducting ring of radius r has charge per unit length . A magnetic field perpendicular to plane of the ring changes at rate Db/dt. Torque experienced by the ring is
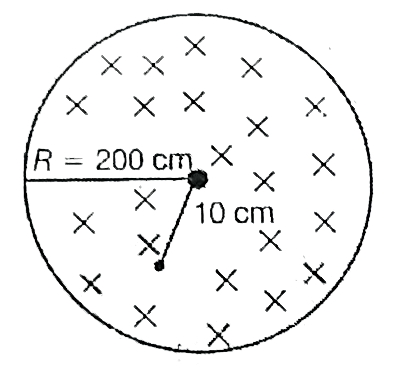
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be . Then the value of k is
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t^(3)T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be (k)/(24) . Then the value of k is
View SolutionA thin conducting ring of radius is given a charge , Fig. The electric field at the center of the ring due to the charge on the part of the ring is . The electric field at the center due to the charge on part of the ring is
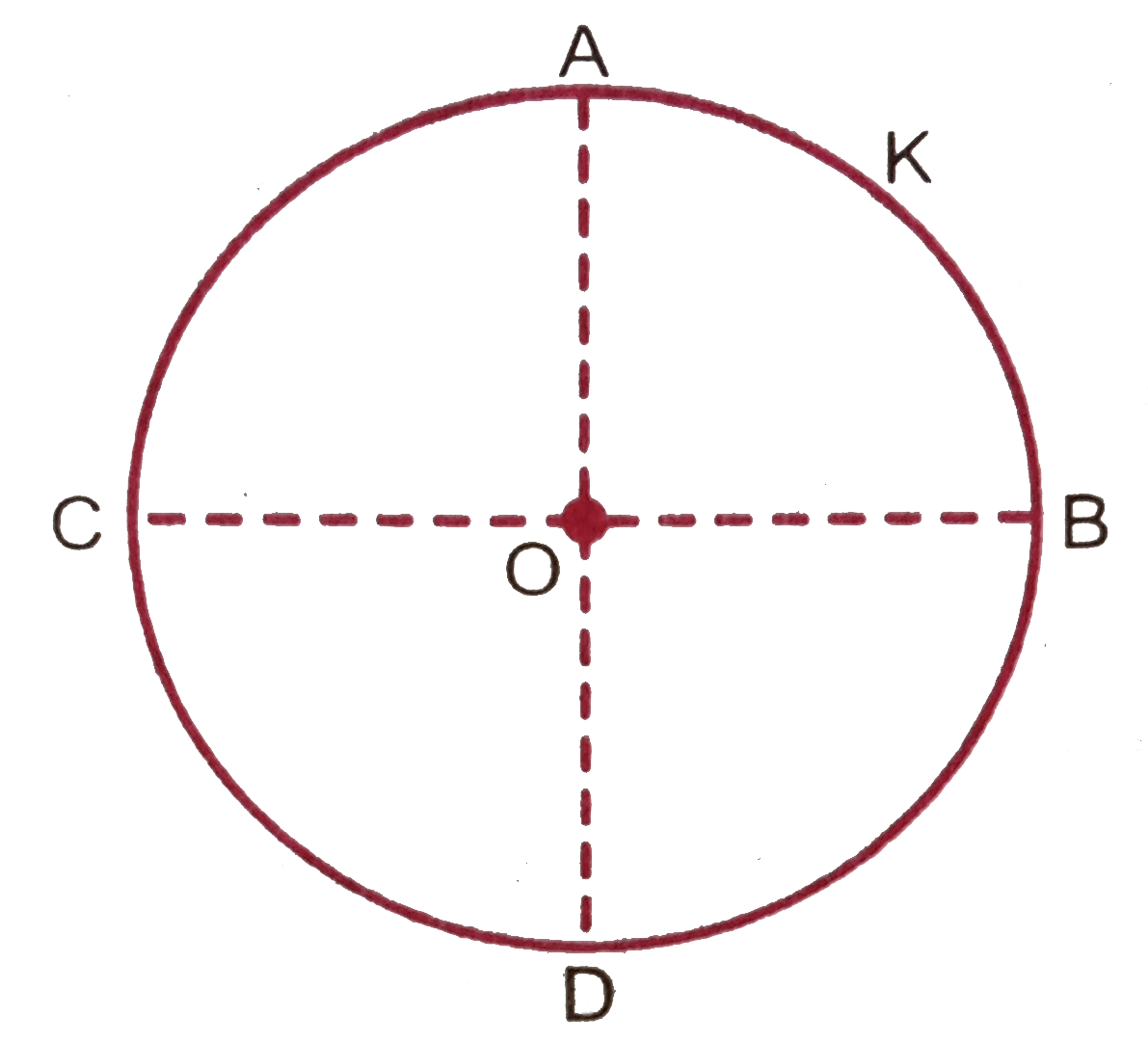
View SolutionA thin conducting ring of radius R is given a charge +Q , Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E . The electric field at the center due to the charge on part ACDB of the ring is
View SolutionA thin conducting ring of radius R is given a charge +Q. The electric field at the centre o of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on the part ACDB of the ring is
View SolutionA thin non-conducting ring of radius R has a linear charge density lambda=lambda_(0)cosphi, where lambda_(0) constant and phi is the azimuthal angle. Find the magnitude of the electric field at the centre at the ring.
View SolutionA half ring of radius R has a charge of lambda per unit length. The electric force on 1C charged placed at the center is
View SolutionA thin conducting ring of radius R is given a +Q charge. The electric field at the center O is E due to the charge on the part AKB of the ring. So the electric field at the center due to the charge on the part ACDB of the ring will be
View SolutionA thin conducting ring of radius R is given a change +Q . The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on the part ACDB of the ring is:
View SolutionA thin conducting ring of radius R is given a charge +Q. The electric field at the centre O of the ring due to the charge on the part ABCD of the ring is
View SolutionThe semicircular non - conducting ring of radius R containing +ve and negative charge as shwon are joined in tw perpendicular planes. The magnitude of linear charge densities is unifrom and is . The electric field at O will be :

View SolutionThe semicircular non - conducting ring of radius R containing +ve and negative charge as shwon are joined in tw perpendicular planes. The magnitude of linear charge densities is unifrom and is . The electric field at O will be :

View Solution