In a acute-angled triangle ABC ∠ABC is the largest angle. The perpendicular bisector of BC and BA intersect AC at X and Y respectively. Prove that the circumcentre of triangle ABC is incentre of triangle BXY.
Let D and E be the mid - points of BC and AB respectively. Since X lies on the perpendicular bisector of BC we have XB = XC. Since XD ⊥ BC and XB = XC it follows that XD bisects ∠ BXC. Similarly YE bisects ∠BYA. Hence the point of intersection of XD and YE is the incentre of Δ BXY but this point of intersection is also the circumcentre of ΔABC being the point of intersection of perpendicular bisectors of BC and AB.
Related Solutions
In any triangle ABC, if the angle bisector of and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
View SolutionIn any triangle ABC, if the angle bisector of and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
View SolutionIn any triangle ABC, if the angle bisector of and perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
View SolutionIn any triangle ABC, if the angle bisector of and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
View Solutionमें का समद्विभाजक AD भुजा BC पर लम्ब है (आकृति देखिये) दर्शाइए की AB=AC है और समद्विभाजक है।
View SolutionIn any triangle ABC, if the angle bisector of and perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
View Solutionमें, का समद्विभाजक AD भुजा BC पर लम्ब है। दर्शाइए कि AB = AC है और समद्विबाहु है।
View Solutionਵਿੱਚ, ਦਾ ਸਮਦੁਭਾਜਕ AD,ਭੁਜਾ BC ਤੇ ਲੰਬ ਹੈ (ਦੇਖੋ ਚਿਤਰ 7.27)। ਸਿਧ ਕਰੋ ਕਿ AB = AC ਅਤੇ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ।
View SolutionIf in a , the bisector AD of angle A is perpendicular to side then is______ triangle.
View SolutionABC is a right triangle such that AB=AC and bisector of angle C intersects the side AB at D. prove that AC+AD=BC.
View SolutionIn ABC, AB = AC and the bisector of intersects BC at D. Prove that, ( 1 )
View Solutionएक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AC = BC यदि है तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है |
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है । यदि है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है ।
View Solutionयदि ABC एक समद्विबाहु त्रिभुज है तथा AC = BC यदि है तो सिद्ध कीजिए कि एक समकोण त्रिभुज है |
View SolutionABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। यदि है, तो सिद्ध कीजिए कि त्रिभुज ABC एक समकोण त्रिभुज है।
View Solutionలో AD అనేది BC భుజామునకు లంబ సమద్విఖండన రేఖ. , AB=AC అయ్యేటట్లున్న సమద్విబహు త్రిభుజామని చూపండి.
View Solutionमें AD भुजा BC का लम्ब समद्विभाजक है। दर्शाइए कि एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
View Solutionमध्ये चा दुभाजक, बाजू BC वर लंब असेल तर सिद्ध करा की हा समदिभुज त्रिकोण आहे.
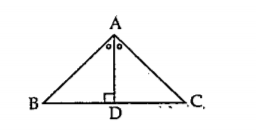
View Solutionमें, समकोण हैं। भुजा AC पर BD लम्ब हैं, तो सिद्ध कीजिए कि के समरूप है।
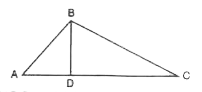
View SolutionIn , the bisector AD of is perpendicular to side BC (see Fig. 7.27). Show that AB = AC and is isosceles.
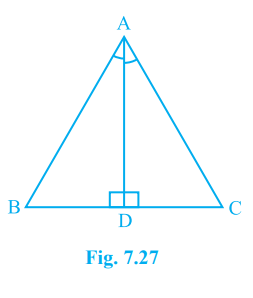
View Solution