If R is the point of intersection of the line L with the line x = 1 then A R lies inside both C and E B R lies outside both C and E C R lies on both C and E D R lies inside C but outside E
Use the position of a point w.r.t a circle. Coordinates of R are 1 2
Related Solutions
Let be the ellipse and be the circle . Let be the points (1, 2) and (2, 1), respectively. Then, (a) lies inside but outside (b) lies outside both (c) lies inside both and (d) lies inside but outside
View SolutionLet E be the ellipse (x^2)/9+(y^2)/4=1 and C be the circle x^2+y^2=9 . Let Pa n dQ be the points (1, 2) and (2, 1), respectively. Then (a) Q lies inside C but outside E (b) Q lies outside both Ca n dE (c) P lies inside both C and E (d) P lies inside C but outside E
View SolutionLet be the ellipse and be the circle . Let be the points (1, 2) and (2, 1), respectively. Then lies inside but outside lies outside both lies inside both and lies inside but outside
View SolutionLet be the ellipse and be the circle . Let be the points (1, 2) and (2, 1), respectively. Then lies inside but outside lies outside both lies inside both and lies inside but outside
View SolutionLet be a relation on defined by then show that: for all
View SolutionIn Figure are two points on such that Show that
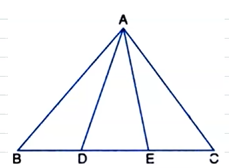
View SolutionIn Figure are two points on such that Show that
View SolutionIf and are two triangles such that , then
View SolutionIn Figure, is a pentagon. A line through parallel to meets produced at Show that:
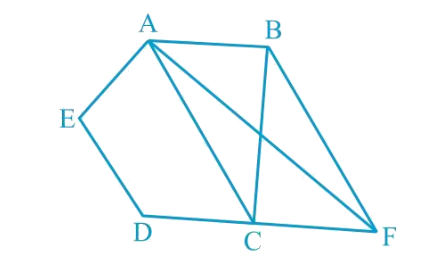
View SolutionIn Figure, is a pentagon. A line through parallel to meets produced at Show that (ii)
View SolutionIn Figure, is a pentagon. A line through parallel to meets produced at . Show that:
(i)
(ii)
View SolutionIn Figure, is a pentagon. A line through parallel to meets produced at . Show that: (i) (ii) quadrilateral
View Solutionint(sum_(r=0)^(oo)(x^(r)backslash2^(r))/(r!))dx=(A)e^(x)+C(B)(e^(2x))/(2)+C(C)-(2)/(1-2x)+C(D)2e^(2x)+C
View SolutionIn , and are altitudes. Prove that
View Solutionis a line parallel to side of . and meet in and respectively. Show that .
View SolutionIn Figure, and are on the same base . If and intersect at , prove that .
View SolutionAny point is taken in the base of a triangle is produced to making equal to . Show that
View SolutionIf d is the distance from a point P to the center of the circle of radius r and , then the point P lies………… the circle. (outside/inside/on)
View SolutionAny point is taken in the base of a triangle is produced to making equal to Show that
View Solutionis a parallelogram, is the point on such that is a point of such that and is the point of such that Prove that:
View Solution