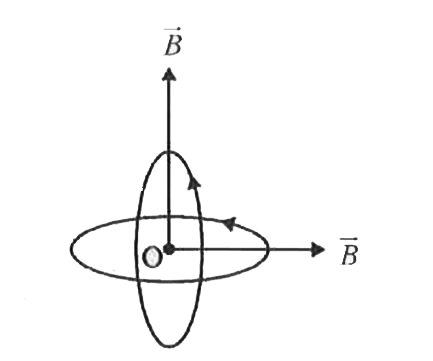
Two similar coils are kept mutually perpendicular such that their centers co-inside. At the centre find the ratio of the mag. field due to one coil and the resultant magnetic field by both coils if the same current is flown. a 1 : √2 b 1 : 2 c 2 : 1 d √3 : 1
The correct option a 1 : √2 Explanation:Both coils are similar For the coil B = μ0I/2rhence B1 = μ0I/2r B2 = μ0I/2rBoth coils are perpendicularhence Bnet = √B12 + B22 = √2B12 = √2 B1∴ ratio of Bnet/B1 = √2i.e. [mag. field due to one coil/resultant mag. field] = B1/Bnet= 1/√2
Related Solutions
Two similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View Solutionदो समरूप कुण्डलियों में, जिनके केंद्र उभयनिष्ठ है, समान विद्युत धारा बहती है। इसके तल परस्पर लंबवत है। यदि केवल एक कुण्डली के कारण केंद्र, पर चुंबकीय क्षेत्र B है, तो केंद्र पर परिणामी चुंबकीय क्षेत्र का मान होगा :
View Solutionदो समरूप कुण्डलियों को इस तरह से रखा गया हैं कि उनके केन्द्र एकसमान हैं। समान धारा के लिए केन्द्र पर पहली कुण्डली एवं दोनों कुण्डली के परिणामी चुम्बकीय क्षेत्र का अनुपात है
View Solutionदो संकेन्द्रिय कुण्डलियों में समान की धारा 1 ऐम्पियर एक ही दिशा में प्रवाहित हो रही है तथा दोनों कुण्डलियों में फेरों की संख्या 100 है। यदि पहल कुण्डली की त्रिज्या 5 सेमी तथा दूसरी कुण्डली की त्रिजया 15 सेमी हो तो केंद्र पर उत्न्थ चुम्बकीय क्षेत्र का मान ज्ञात करो। यदि दूसरी कुण्डली में धारा की दिशा विपरीत कर दी जाए तो केंद्र पर परिणामी चुम्बकीय क्षेत्र ज्ञात करो।
View Solutionएक धारावाही वृत्ताकार कुंडली (कुंडली 1) और एक चकती के एक चौथाई के समान आकार वाली एक बंद कुंडली (कुंडली 2) के केंद्र पर चुंबकीय क्षेत्र प्रेरण, परिमाण में बराबर पाया जाता है। यदि दोनों कुंडलियों का क्षेत्रफल बराबर है, तो कुंडली 2 और कुंडली 1 में प्रवाहित धाराओं का अनुपात ज्ञात कीजिए।
View SolutionThe magnetic field induction at the centre of a current - carrying circular coil (coil 1) and a closed coil (coil 2), shaped as a quarter of a disc is found to be equal in magnitude. If both the coils have equal area, then find the ratio of the currents flowing in coil 2 and coil 1.
View SolutionThe magnetic field induction at the centre of a current - carrying circular coil (coil 1) and a closed coil (coil 2), shaped as a quarter of a disc is found to be equal in magnitude. If both the coils have equal area, then find the ratio of the currents flowing in coil 2 and coil 1.
View SolutionThe ratio of the magnetic field at the centre of a current carrying coil of the radius and at distance from centre of the coil and perpendicular to the axis of coil is
View SolutionThe ratio of the magnetic field at the centre of a current carrying coil of the radius a and at distance 'a' from centre of the coil and perpendicular to the axis of coil is
View SolutionTwo concentric coils carry the same current in opposite directions. The diameter of the inner coil is equal currents. The outer coil. If the magnetic field produced by the outer coil at the common centre are , the net field at the centre is
View Solutionचित्र के अनुसार दो समरूप कुण्डलियों में समान विद्युत धारा प्रवाहित हो रही है। कुण्डलियों के केंद्र उभयनिष्ठ तथा तल परस्पर लम्बवत है। यदि एक कुण्डली के कारण इसके केंद्र पर चुम्बकीय क्षेत्र B है तो उभयनिष्ठ केंद्र पर परिणामी चुम्बकीय क्षेत्र का मान होगा।
View Solutiona current is flowing in a circular coil of radius I. At what distance from the center on the axis of the coil will the magnetic field be 1/8th of the magnetic field at the centre.
View SolutionMagnetic Field At Centre Due To Current Carrying Coil |Magnetic Field On Axis Due To Current Carrying Coil|OMR
View Solutionकिसी R त्रिज्या की वृत्तीय कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का मान है। 2R त्रिज्या की दूसरी कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का मान है, का अनुपात होगा :-
View SolutionThe ratio of the inductances of two coils is 1 : 2 and that of the currents through them is 2 : 1. Find the ratio of energy stored in the coils.
View SolutionThe resultant magnetic field at the center will be because of the square BC of the square coil shown in the picture, the magnetic field at the center of the coil is B:
View SolutionThe radius of a current carrying coil is R. The ratio of the magnetic field at an axial point at a distance R from the center of the coil and the magnetic field at the center of the coil is -
View SolutionTwo circular coils 1 and 2 are made from the same wire but the radius of the 1st coil is twice that of the 2nd coil. What is the ratio of potentail difference applied across them so that the magnetic field at their centres is the same?
View Solution