One end of a rod of length L = 1 m is fixed to a point on the circumference of a wheel of radius R = 1/ √3 m. The other end is sliding freely along a straight channel passing through the center O of the wheel as shown in the figure below. The wheel is rotating with a constant angular velocity ω about O.The speed of the sliding end P when θ = 60° isA 2ω/3B ω/3C 2ω/√3D ω/√3
Correct option A 2ω/3Explanation:
Related Solutions
One end of a rod of length L is fixed to a point on the circumference of a wheel of radius R. The other end is sliding freely along a straight channel passing through the centre O of the wheel as shown in the figure below. The wheel is rotating with a constant angular velocity about O. Taking the motion of the rod is
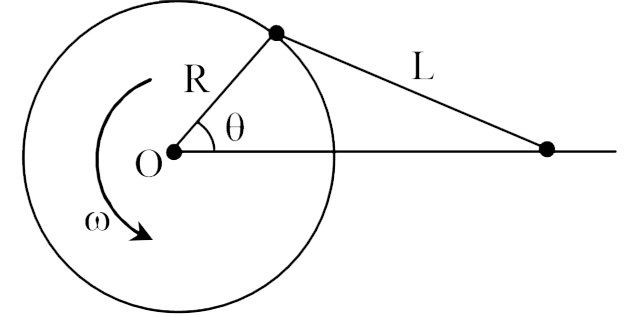
View SolutionOne end of a rod of length L=1 m is fixed to a point on the circumference of a wheel of radius m. The other end is sliding freely along a straight channel passing through the center O of the wheel as shown in the figure below. The wheel is rotating with a constant angular velocity about O.

The speed of the sliding end P when is
View Solutionएक पहिया जमीन के अनुदिश 2 मी/से के वेग से लुढ़क रहा है पहिये के क्षैतिज व्यास के सिरों पर स्थित बिंदुओं के वेग का परिमाण है
View Solutionएक पहिया जमीन के अनुदिश 2 मी/से के वेग से लुढ़क रहा है। पहिये के क्षैतिज व्यास के सिरों पर स्थित बिन्दुओं के वेग का परिमाण है
View SolutionA bicycle wheel (ring) of mass 1kg and radius 2m is attached at the end of a long rod of mass 1kg and length 3m, with the axis of wheel perpendicular to the rod. The rod is rotating counter clockwise as seen from above about its other end with an angular speed 0.5 rad/s. If wheel is also rotating about its axis with same angular speed in counter clock wise sense as seen from above. Find angular momentum of the system (in kg-m/s) about the axis passing through one end of rod. (Neglect mass of spokes and mass of rod connecting end of length 3m and centre of ring).
View SolutionA wheel of radius 0.5 m rotates with a constant angular speed about an axis perpendicular to its center. A point on the wheel that is 0.2 m from the center has a tangential speed of 2 m/s.
Determine the tangential speed of a point 0.4 m from the center of the wheel.
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity omega in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity omega in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
View SolutionA chord is tied to a wheel of moment of inertia and radius . The other end is attached to a mass as shown. If the mass falls by a height then the square of angular speed of the wheel is ?
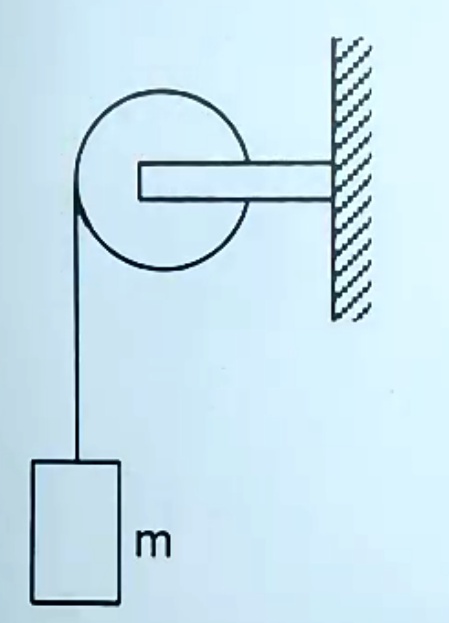
View SolutionA cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and is . A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
View SolutionA cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and MI is I . A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :

View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :
View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :
View SolutionIf a point on the circumference of a wheel having diameter 4 m has velocity of 1600 c, then the angular velocity of the wheel will be
View SolutionA wheel of radius 0.1 m (wheel A) is attached by a non-stretching belt to a wheel of radius 0.2 m (wheel B). The belt does not slip. By the time wheel B turn through 1 revolution, wheel A will rotate through:
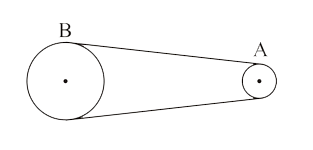
View SolutionA wheel of radius 0.1 m (wheel A) is attached by a non-stretching belt to a wheel of radius 0.2 m (wheel B). The belt does not slip. By the time wheel B turn through 1 revolution, wheel A will rotate through:

View SolutionAs shown in the figure 1 m Perpendicular to the plane of the circular conductor ring of radius 1 T As much as the magnetic field is applied. In the plane of this ring 1 m A conductor rod of length, one end of which is fixed at the center of the ring and the other end in contact with the circumference of the ring, rotates at a constant angular speed of 50 rotations / second. So find the induced emf between the two ends of this rod (or between the center and circumference of the ring).
View SolutionA wheel rotates with a constant angular velocity of 300 rpm. The angle through which the wheel rotates in 1 s is.
View SolutionA wheel rotates with a constant angular velocity of 300 rpm. The angle through which the wheel rotates in 1 s is.
View Solution