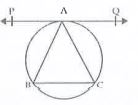
Let BC be a fixed line segment in the plane. The locus of a point A such that the triangle ABC is isosceles is with finitely many possible exceptional pointsA a lineB a circle C the union of a circle and a lineD the union of two circles and a line
Correct option D the union of two circles and a line Explanation:Case i : If ∠B = ∠Clocus of A is ⊥ bisector of BCSo it is straight lineCase ii :If ∠A = ∠CBC fixed Ba 0 C0 aBC = ABSo x – a2 + y2 = 2a2 CircleCase iii : ∠A = ∠BAC = BC√h2 + k - a2 = √2a2x2 + y – a2 = 2a2 also a circleSo union of two circle and a line.
Related Solutions
Let BC be a fixed line segment in the plane . The locus of a point A such that the triangle ABC is isosceles , is (with finitely many possible exceptional points )
View Solutionयदि किसी त्रिभुज ABC के परिगत एक वृत्त खींचा जाए, तथा A बिंदु पर खींची गई स्पर्श रेखा आधार BC के समांतर हो, तो सिद्ध कीजिए कि समद्विबाहु है।
View SolutionA circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point , the locus of the centre of the circle, is
View SolutionA circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point , the locus of the centre of the circle, is
View SolutionThe locus of the centre of the circles (in a plane) passing through two given points is the ______ of the line segment joining the two points.
View SolutionLet P be a variable point on a circle C and Q be a fixed point outside C. If R is the midpoint of the line segment PQ, then locus of R is
View SolutionPQ वृत्त के बिन्दु P पर वृत्त की स्पर्श रेखा हैं। वृत्त का केन्द्र O हैं। यदि एक समद्विबाहु त्रिभुज हैं तो हैं-
View Solutionवृत्त के केंद्र से होकर, वृत्त पर कोई दो बिंदुओं को मिलाने वाली रेखाखंड को . . . . . . . . .कहते है |
View SolutionA ____ of a circle is a line segment which joins any two points on the boundary of the circle
View SolutionA ____ of a circle is a line segment which joins any two points on the boundary of the circle
View SolutionA ____ of a circle is a line segment joining any two points on the circle.
View SolutionThe line segment joining two points on a circle is called the ...... of the circle.
View SolutionLine PQ is a tangent to the circle at point A, . Prove that is isosceles triangle.
View SolutionTake two points A and C on the circle, them the line segment joining the point A and C is called a ………... of the circle.
View Solutionसिद्ध कीजिए कि किसी वृत्त की दो समांतर स्पर्श रेखाओं के स्पर्श बिंदुओं को मिलाने वाली रेखा खंड वृत्त का व्यास होता है।
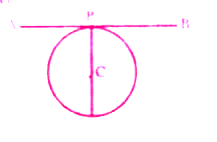
View SolutionAB Is a fixed line segment. Prove that the point P The locus of will be a circle whose diameter AB Is if angle APB = 90° Ho.
View SolutionDraw and name :Draw a circle and a line such that the line intersects the circle at two point.
View SolutionIf the straight line intersects the circle at two points, then the straight line is called a to the circle.
View SolutionA and B are two fixed points and the line segment AB always subtends an acute angle at a variable point P .Show that the locus of the point P is a circle.
View SolutionIf the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is a square (b) a circle a straight line (d) two intersecting lines
View Solution