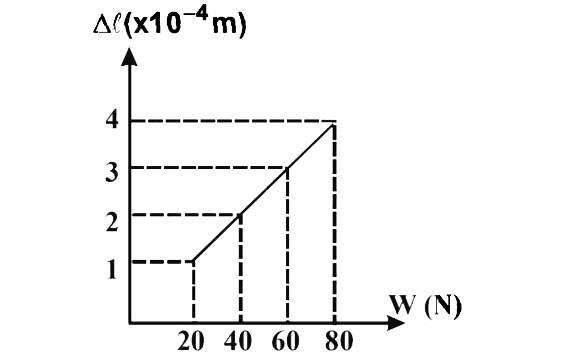
The adjacent graph shows the extension of a wire of length 1 m suspended from the top of a roof at one end with the load W connected to the other end. If the cross sectional area of the wire is 10–6 m2 calculate the youngs modulus of the material of the wire. A 2 × 1011 N / m2 B 2 × 10–11 N / m2 C 2 × 10–12 N / m2 D 2 × 10–12 N / m2
Correct option: A 2 × 1011 N/m2Explanation: From the graph ℓ = 1 × 10–4 mF = 20 NA = 10–6 m2 L = 1 mY = FL / Aℓ= {20 × 1 / 10–6 × 10–4}= 20 × 1010 = 2 × 1011 Nm–2
Related Solutions
The adjacent graph shows the extension (DeltaI) of a wire of length 1 m suspended from the top of a roof at one end with a load W connected to the other end. If the cross-sectional area of the wire is 10^(-6) m ^(2), calculate The Young's modulus of the material of the wire is ........
View SolutionThe graph shows the extension of a wire of length 1m suspended from the top of a roof at one end with a load W connected to other end if the cross sectional area of wire is , calculate the young's modulus of the material of the wire.
View SolutionThe adjacent graph shows the extension of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is calculate the young's modulus of the material of the wire .

View SolutionThe adjacent graph shows the extension Deltal of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 10^(6) m^(2) calculate the young's modulus of the material of the wire .
View SolutionThe adjacent graph shows the extension Deltal of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 10^(6) m^(2) calculate the young's modulus of the material of the wire .
View SolutionA wire of length 1 m and area of cross section 2xx10^(-6)m^(2) is suspended from the top of a roof at one end and a load of 20 N is applied at the other end. If the length of the wire is increased by 0.5xx10^(-4)m , calculate its Young’s modulus (in 10^(11)N//m^(2)) .
View SolutionA wire of length 1 m and area of cross section is suspended from the top of a roof at one end and a load of 20 N is applied at the other end. If the length of the wire is increased by , calculate its Young’s modulus (in .
View SolutionThe adjacent graph shows the estension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is , calculate the Young's modulus of the material of the wire.
View SolutionThe adjacent graph shows the estension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is , calculate the Young's modulus of the material of the wire.

View SolutionThe adjacent graph shows the estension (Deltal) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10^-6m^2 , calculate the Young's modulus of the material of the wire.
View SolutionA elongation of 0.1% in a wire of cross-sectional area 10"6 m2 causes tension 100 N. The young’s modulus is
View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1 mm^(2) , then the Young's modulus of the material of the wire. ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_RACE_R64_E01_001_Q01.png" width="80%"gt
View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1 mm^(2) , then the Young's modulus of the material of the wire. ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_RACE_R64_E01_001_Q01.png" width="80%"gt
View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1 mm^(2) , then the Young's modulus of the material of the wire. ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_RACE_R64_E01_001_Q01.png" width="80%"gt
View SolutionThe adjacent graph shows the extra extension (Deltax) of a wire of length 1m suspended from the top of a roof at one end with an extera load Deltaw connected to the other end If the cross sectional area of the wire is 10^(-5)m^(2) calculate the Young's modulus of the meterial of the wire (A) 2 xx 10^(11) N//m^(2) (B) 2 xx 10^(-11)N//m^(2) (c) 3 xx 10^913) N//m^(3) (D) 2 xx 10^(16)N//m^(2) .
View SolutionThe adjacent graph shows the extra extension (Deltax) of a wire of length 1m suspended from the top of a roof at one end with an extera load Deltaw connected to the other end If the cross sectional area of the wire is 10^(-5)m^(2) calculate the Young's modulus of the meterial of the wire (A) 2 xx 10^(11) N//m^(2) (B) 2 xx 10^(-11)N//m^(2) (c) 3 xx 10^913) N//m^(3) (D) 2 xx 10^(16)N//m^(2) .
View SolutionYoung.s modulus of a wire is . If a stress of 2 x 108 N/m2 is applied at the free end of a wire, find the strain in the wire.
View SolutionYoung.s modulus of a wire is . If a stress of 2 x 108 N/m2 is applied at the free end of a wire, find the strain in the wire.
View SolutionA wire of length 2m is tightened at one end and a force of 10N is applied at the other end. area of cross section of wire 2 xx 10^(-6)m^(2) and Young's coefficient of the material of the wire 2xx 10^(11)N m^(-2) Is. Calculate the increase in the length of the wire.
View SolutionA 1 m long metal wire of cross sectional area is fixed at one end from a rigid support and a weight W is hanging at its other end. The graph shows the observed extension of length of the wire as a function of W. young’s modulus of material of the wire in SI units is :

View Solution