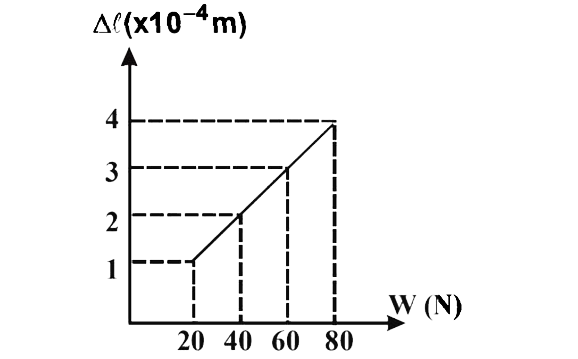
The adjacent graph shows the extension Deltal of a wire of length 1m

The adjacent graph shows the estension $(Δ l)$ of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is $10^{- 6} m^{2}$ , calculate the Young's modulus of the material of the wire.

A(a) $2 \times 10^{11} N / m$
B(b) $2 \times 10^{- 11} N / m$
C(c) $3 \times 10^{- 12} N / m$
D(d) $2 \times 10^{- 13} N / m$
A wire of length 10 m and cross-section are $10^{- 6} m^{2}$ is stretched with a force of 20 N. If the elongation is 1 mm, the Young's modulus of material of the wire will be
A $10^{10} N / m^{2}$
B $10^{11} N / m^{2}$
C $2 \times 10^{10} N / m^{2}$
D $2 \times 10^{11} N / m^{2}$
A load of $3 k g$ produces an extension of $1.5 m m$ in a wire of length $3 m$ and diameter $2 m m$ . Young's modulus of the material of the wire is
A $1.87 \times 10^{10} N m^{- 2}$
B $3.5 \times 10^{10} N m^{- 2}$
C $15 \times 10^{10} N m^{- 2}$
D $2.5 \times 10^{10} N m^{- 2}$

The adjacent graph shows the extension $Δ l$ of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is $10^{6} m^{2}$ calculate the young's modulus of the material of the wire .