When a mass m is suspended from the free end of a massless spring having force constant k its oscillates with frequency f. Now if the spring is divided into two equal parts and a mass 2m is suspended from the end of anyone of them it will oscillate with a frequency equal to………A f B 2f C f/√2 D √2f
The correct option A fExplanation:f = 1/2π √k/mnow spring is divided in two equal parts & mass 2m is suspended let new frequency is f. New spring constant of each part be Kas Kℓ is constant∴ kℓ = k ℓ/2∴ k = 2k∴ f = 1/2π √2k/2m = f
Related Solutions
A massless spring, having force constant k, oscillates with a frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass 2m is suspended from one of the parts. The frequency of oscillation will now be………….
View SolutionA massless spring, having force constant k, oscillates with frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass 2m is suspended from one half. The frequency of oscillation will now be
View SolutionA weightless spring which has a force constant k oscillates with frequency n when a mass m is suspended from it The spring is cut into two equal halves and a mass 2m is suspended from it. The frequency of oscillation will now become
View SolutionA weightless spring has a force constant k oscillates with frequency f when a mass m is suspended from it The spring is cut into three equal parts and a mass 3 m is suspended from it The frequency of oscillation of one part will now become
View SolutionA weightless spring has a force constant k oscillates with frequency f when a mass m is suspended from it The spring is cut into three equal parts and a mass 3 m is suspended from it The frequency of oscillation of one part will now become
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View Solutionजब एक भारहीन व k बल नियतांक वाली स्प्रिंग पर m द्रव्यमान का पिण्ड लटकाया जाता है तब यह n आवृति से दोलन करता है। स्प्रिंग को दो बराबर भागो में काटा जाता है। स्प्रिंग के एक भाग पर 2m द्रव्यमान का पिण्ड लटकाया जाता है। अब दोलनों की आवृति होगी
View SolutionA mass hangs at the end of a massless spring and oscillates up and down at its natural frequency f. If the spring is cut at the midpoint and and mass reattached at the end, the frequency of oscillation is :
View SolutionA spring has a force constant k and a mass m is suspended from it the spring is cut in two equal halves and the same mass is suspended from one of the halves. If the frequency of oscillation in the first case is n, then the frequency in the second case will be
View SolutionA mass suspended from a spring of spring constant k is made to oscillate with a time period T. Now, the spring is cut into three equal parts and the mass is suspended from one of the parts. What will be the new time period of oscillations?
View Solutionk બળઅચળાંકવાળી અને વજનરહિત સ્પ્રિંગ ના છેડે m દળ લટકાવી દોલિત કરતાં f આવૃત્તિથી દોલનો કરે છે. હવે, જો સ્પ્રિંગના બે સમાન ટુકડા કરવામાં આવે અને કોઈ એક ટુકડાના છેડે 2 m દળ લટકાવી સરળ આવર્ત દોલનો મેળવવામાં આવે, તો આવૃત્તિ f’ = ........ .
View SolutionA mass m is suspended from a spring of force constant k. The period of oscillation is The spring is cut into 4 equal parts: The same mass m is suspended from one of the parts. What is the new period?
View SolutionA mass is suspended from the end of a spring. When the system is oscillating the amplitude of oscillation is 4 cm and maximum kinetic energy of oscillation of the system is 1J. Then the force constant of the spring is
View SolutionTwo identical springs, each of spring constant K, are connected first series and then in parallel. A mass M is suspended from them. The ratio of the frequencies of vertical oscillations will be :
View SolutionOn suspending a mass m from a spring of force constant k, frequency of vibration f is obtained. If a second spring as shown in the figure, is arranged then the frequency will be :
View SolutionA spring of force constant is cut into two equal parts, and mass 'm' is suspended from parallel combination of the springs. Then frequency of small osciollations is
View SolutionK बल नियतांक की एक स्प्रिंग से M द्रव्यमान को लटका कर दोलन कराने पर दोलन आवृत्ति f प्राप्त होती है। यदि दूसरी स्प्रिंग को चित्रानुसार व्यवस्थित कर दी जाये तो आवृत्ति हो जायेगी:
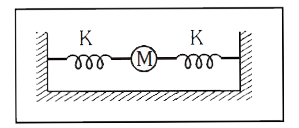
View SolutionA spring is connected to a mass m suspended from it and its time period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is
View SolutionA spring is connected to a mass m suspended from it and its time period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves . The period of vertical oscillation is
View Solution