Surface mass density of disc of mass m and radius R is σ = Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :1 I = 3/2 mR22 I = 4/3mR23 I = 2/5mR24 I = 2/3mR2
Related Solutions
Surface mass density of disc of mass and radius is . Then its moment of inertia axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionSurface mass density of disc of mass m and radius R is Kr^(2) . Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionA solid sphere of mass M and radius R having moment of inertia about an axis passing through the centre of mass as I, is recast into a disc of thickness I, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains I. Then, radius of the disc will be
View SolutionM द्रव्यमान और R त्रिज्या की वृत्ताकार चकती में से m द्रव्यमान व त्रिज्या की एक चकती काट ली जाती है। शेष चकती के लिए उसके द्रव्यमान केन्द्र से गुजरने वाले तल के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण होगा-
View SolutionM द्रव्यमान और R त्रिज्या की वृत्ताकार चकती में से m द्रव्यमान व त्रिज्या की एक चकती काट ली जाती है। शेष चकती के लिए उसके द्रव्यमान केन्द्र से गुजरने वाले तल के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण होगा-
View SolutionA solid sphere of mass M, radius R and having moment of inertia about an axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains I. Then, radius of the disc will be
View SolutionA solid sphere of mass M, radius R and having moment of inertia about an axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains I. Then, radius of the disc will be
View SolutionThe moment of inertia of a quadrant of a uniform disc of radius R and mass M with respect to an axis passing through its center of mass and perpendicular to its plane is:
View SolutionR त्रिज्या और 9M द्रव्यमान वाली एक चकती से R/3 त्रिज्या तथा M द्रव्यमान वाली एक संकेन्द्रीय छोटी चकती निकाली जाती है । शेष बची चकती का उसके तल के लंबवत तथा केंद्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण लेगा -
View Solution1kg द्रव्यमान तथा 2m त्रिज्या की वृत्तीय चकती के तल के लम्बवत्, द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण है। चकती के सतह से गुजरने वाले अक्ष के समानान्तर जड़त्व आघूर्ण होगा (दिये गये चित्रानुसार)
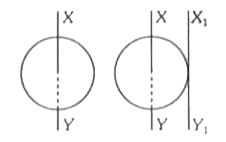
View SolutionFind the rotational kinetic energy of a ring of mass 9 kg and radius 3 m rotating with 240 rpm about an axis passing through its centre and perependicualr to its plane.
View SolutionThe diagram shows a uniform disc of mass & radius '', if the moment of inertia of the disc about the axis is , its moment of inertia about an axis through and perpendicular to the plane of the disc is
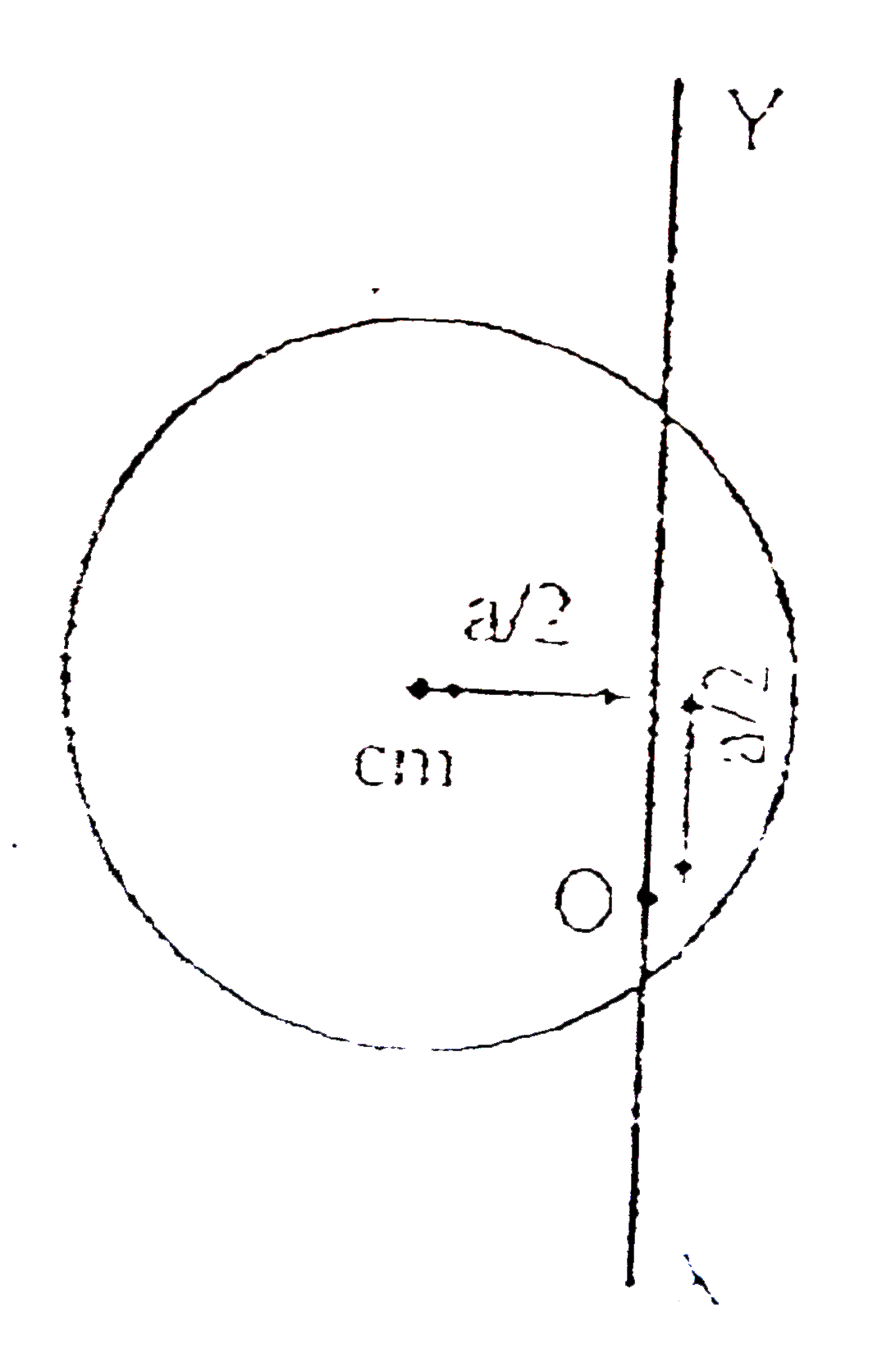
View SolutionThe diagram shows a uniform disc of mass & radius '', if the moment of inertia of the disc about the axis is , its moment of inertia about an axis through and perpendicular to the plane of the disc is
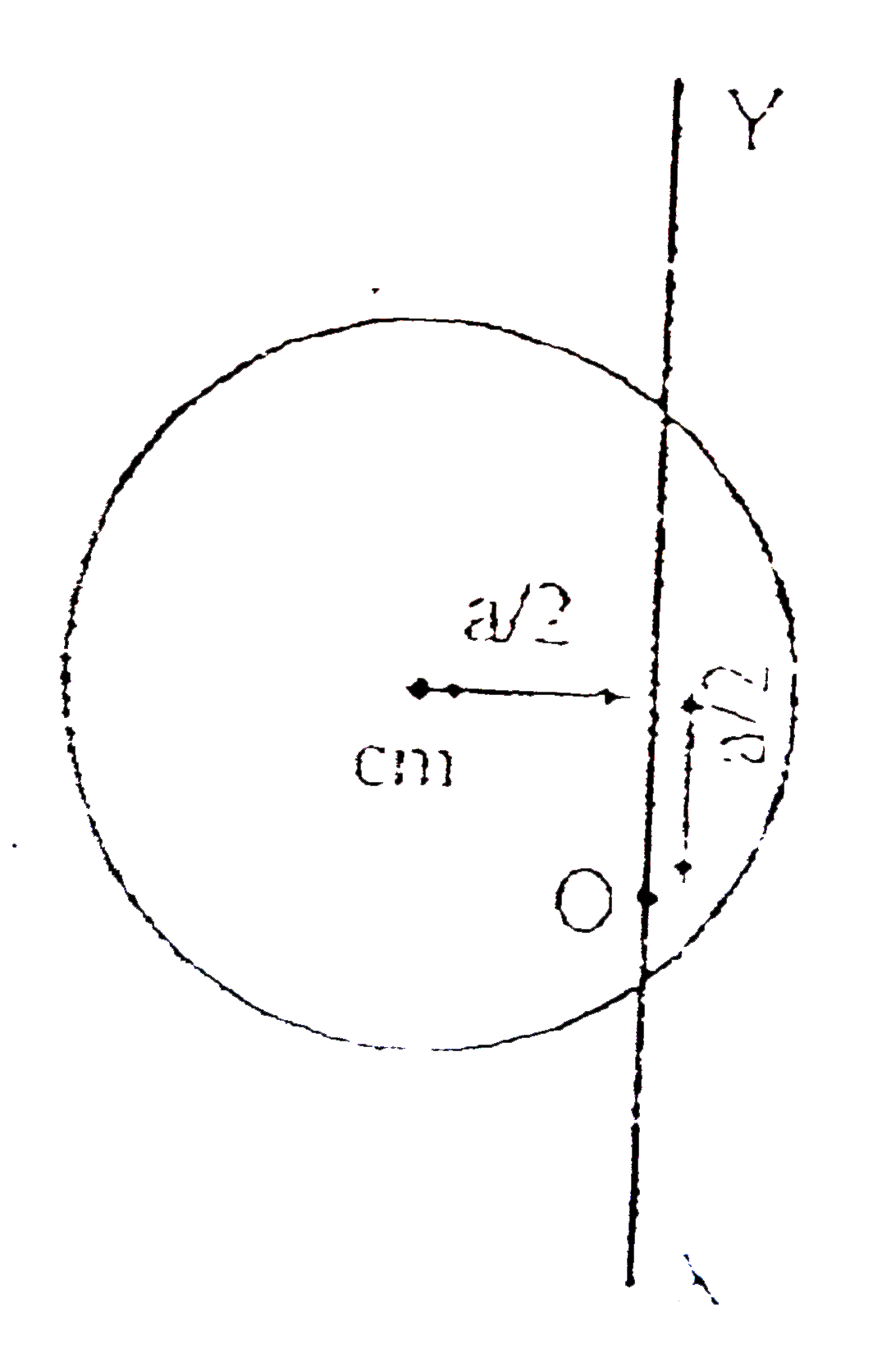
View SolutionThe diagram shows a uniform disc of mass & radius '', if the moment of inertia of the disc about the axis is , its moment of inertia about an axis through and perpendicular to the plane of the disc is
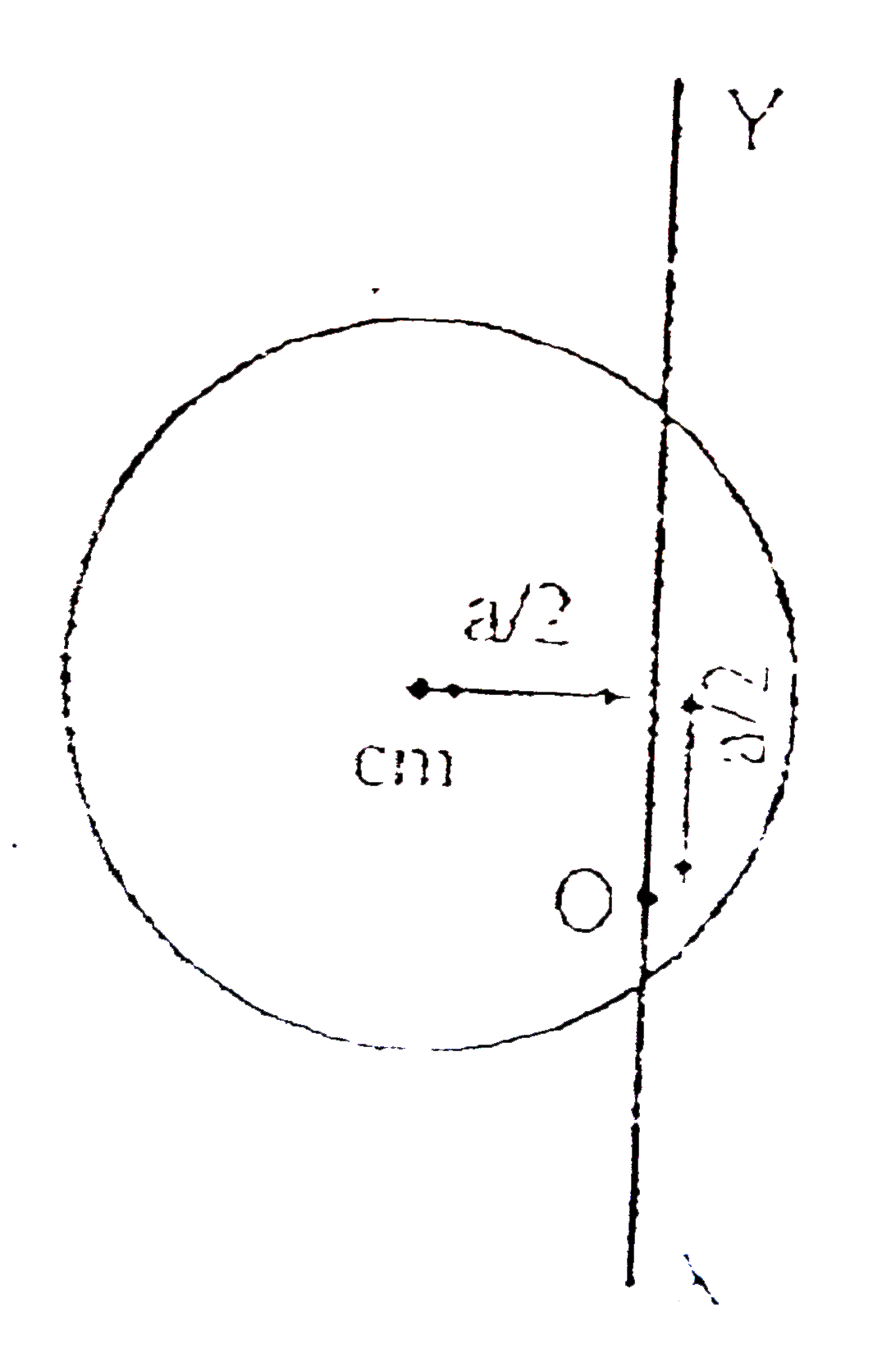
View SolutionA solid sphere of mass , radius and having moment of inertia about as axis passing through the centre of mass as , is recast into a disc of thickness , whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains . Then, radius of the disc will be.
View SolutionA solid sphere of mass , radius and having moment of inertia about as axis passing through the centre of mass as , is recast into a disc of thickness , whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains . Then, radius of the disc will be.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe moment of inertia of a uniform semicircular disc of mass and radius about a line perpendicular to the plane of the disc through the center is
View SolutionThe moment of inertia of a uniform semicircular disc of mass and radius about a line perpendicular to the plane of the disc through the center is
View Solution