Surface mass density of disc of mass and radius is . Then its moment of inertia axis of rotation passing through center and perpendicular to the plane of disc is :
The correct Answer is:D
Step by step video, text & image solution for Surface mass density of disc of mass m and radius R is alpha-Kr^(2). Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View Solution
Knowledge Check
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
A12m(R−r)2B12m(R2−r2)C12m(R+r)2D12m(R2+r2)Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2
Four similar point masses (m each) are symmetrically placed on the circumference of a disc of mass M and radius R. Moment of inertia of the system about an axis passing through centre O and perpendicular to the plane of the disc will be
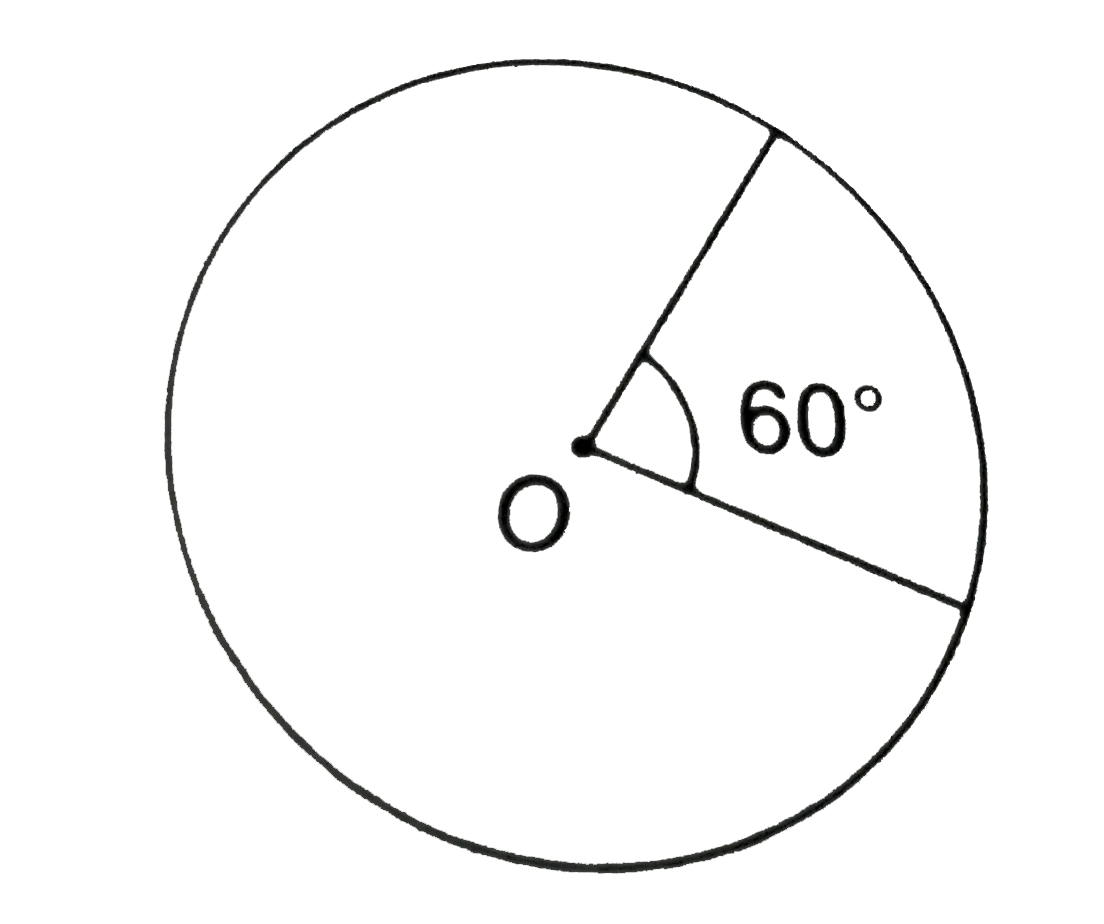
View SolutionFrom a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
View SolutionA circular thin disc of mass 2 kg has a diameter 0.2 m. Calculate its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc (in kg m2)
View SolutionThe diameter of a thin circular disc of mass 2 kg is 0.2 m. Its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc is
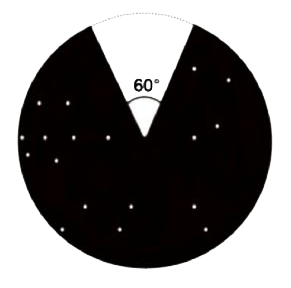
View SolutionThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
View Solution
