If D E F are the mid-points of the sides of a triangle ABC prove by vector method that area of ∆DEF = 1/4 area of ∆ABC.
Taking A as the origin let the position vectors of B and C be vector b and c respectively. Then the position vectors of D E and F are = 1/4 vector area of ∆ABCHence area of ∆DEF = 1/4 area of ∆ABC.
Related Solutions
If D,E,F are the mid-points of the sides BC,Ca and AB respectively of a triangle ABC ,prove by vector method that Area of Delta DEF=1/4 Area of Delta ABC
View SolutionIf D, E, f are the mid-point of the sides of triangle ABC, prove that : .
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of , then the ratio of the areas of to the area of is :
View SolutionIn are respectively the mid points of the sides AB, BC and AC. Find ratio of the area of and area of .
View SolutionIn triangle, ABC the points D,E,F are the midpoints of the sides , BC CA, and AB respectively. Using vector method, show that the area of is equal to .
View SolutionIf D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
View SolutionD,E and F are the mid points of the sides BC, CA and AB respectivley of f then the ratio of the areas of and ABC =………..
View SolutionD, E and F are respectively the mid-points of sides AB, BC and CA of . Find the ratio of the areas of .
View SolutionD,E,F are the mid points of the sides BC, CA and AB respectively of a . Determine the ratio of the areas of and .
View SolutionIn trigle ABC, the points D, E, F are the midpoints of the sides BC,CA, and AB respee. Tively. Using vector methed ,show that the area of DEF is equal to (area of ABC).
View SolutionD, E, F are mid points of sides BC, CA, AB of . Find the ratio of areas of .
View SolutionD, E, F are mid points of sides BC, CA, AB of . Find the ratio of areas of .
View SolutionD, E, F are mid points of sides BC, CA, AB of . Find the ratio of areas of .
View SolutionIf D,E and F respectively Delta ABC If BC are the mid-points of the sides BC, CA and AB, then prove that BDEF is a parallelogram whose area is Delta ABC is half of the area. Also prove that the area Delta DEF = ( 1)/( 4) Area Delta ABC
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of . Prove that:
(i) is a parallelogram
(ii) area of
(iii) area of
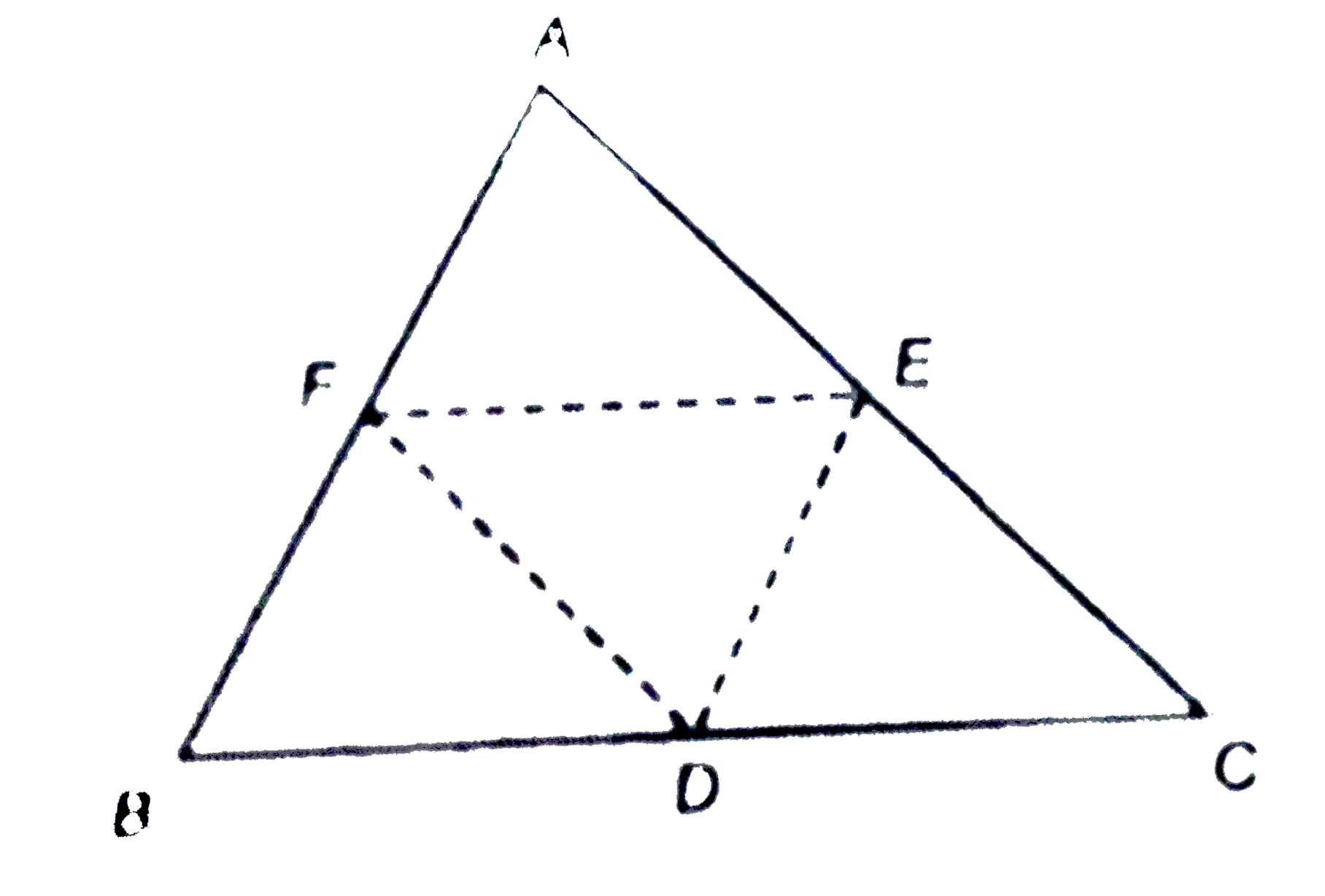
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of . Prove that:
(i) is a parallelogram
(ii) area of
(iii)

View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. show that the area Delta BED = ( 1)/( 4) Area Delta ABC
View SolutionD, E and F are the mid-points of sides of . P, Q, R are the mid-points of sides DEF. This process of marking the mid-points and forming a new triangle is continued. How are the areas of these triangles related?
View Solution