A cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in figure. It hits a ridge at point O. The angular speed of the block after it hits O is …. A 3v / 4a B 3v / 2a C √3v / √2a D zero
Correct option: A 3v / 4aExplanation:when block hits ridge at O it will start rotating about an axis passing through O and perpendicular to the plane of paper. No external torque acts on block hence angular momentum is conserved Angular momentum before hitting Li = M.V × AC= MV ∙ a/2 = [mva / 2]after hitting Lf = IoωIo is MI of block about axis through O and perpendicular to plane of block.if Ic is MI about C then IC = [Ma2 / 6]From parallel axes theorem Io = Ic + Mr2 and r2 = a/22 + a/22 = a2 / 2Io = 1/6Ma2 + 1/2Ma2 = 2/3Ma2 ∴ Lf = 2/3Ma2 ∙ ωalso Li = Lf hence[mva / 2] = 2/3Ma2ω hence ω = 3v / 4a
Related Solutions
A cubical block of side a is moving with velocity v on a horizontal smooth plane as shown. It hits a ridge at point O. The angular speed of the block after it hits O is:
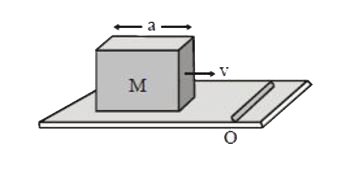
View SolutionA cubical block of side a is moving with velocity v on a horizontal smooth palne as shown . It hits a ridge at point O. The angular sped of the block after it hits O is
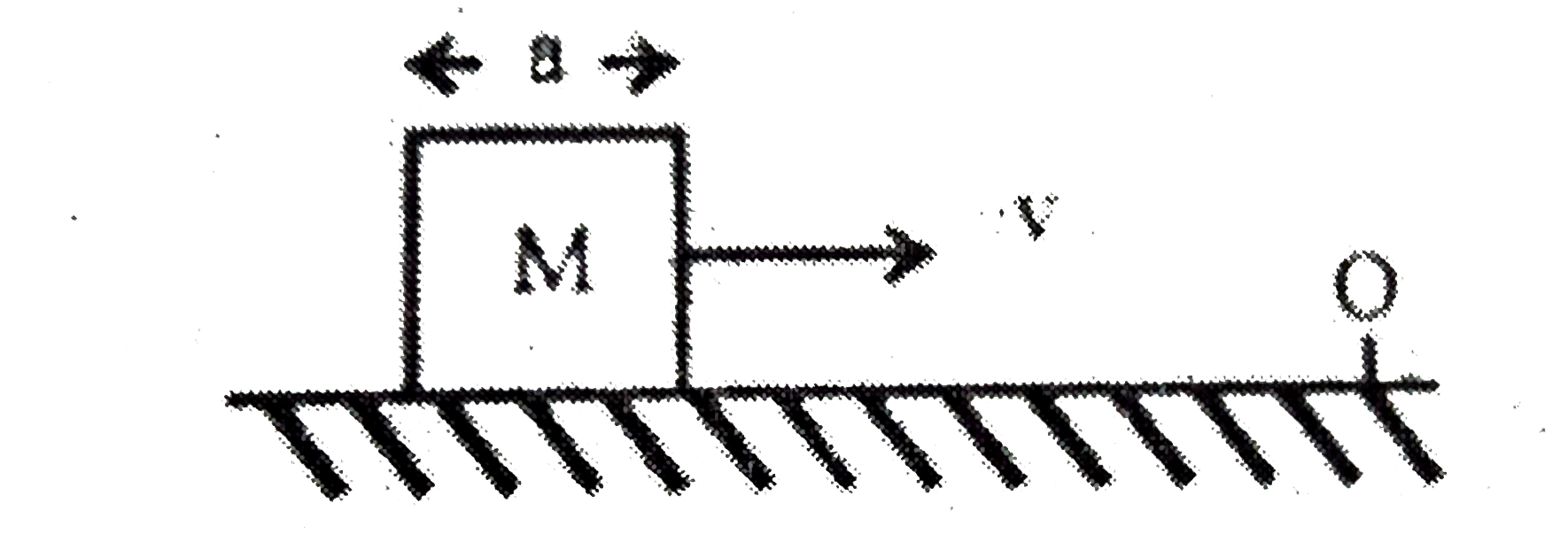
View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed of the block after it hits O is
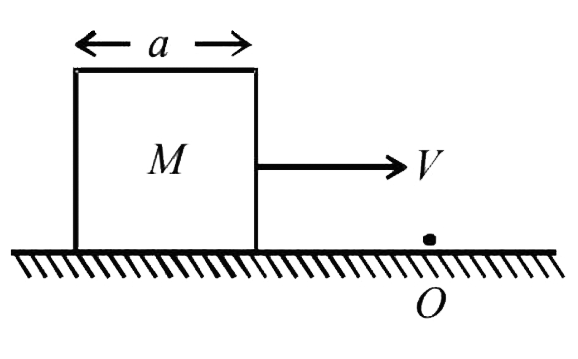
View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed fo the block after it hits O is
View SolutionA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed of the block after it hits O is
View SolutionA cubical block of side a is moving with velocity v on a horizontal smooth plane as shown. It hits a ridge at point O. The angular speed of the block after it hits O is:

View SolutionA cubical block of side 4 cm is moving with 4 m/s on a smooth horizontal plane as shown. It hits a ridge at point O. The angular speed of block after it hits O is , then value of Y is _____ .

View SolutionA cubical block of side a is moving with velocity v on a horizontal smooth plane. It strikes a ridge at point O and sticks to it (collision is completely inelastic) The angular speed of the block after hitting O is
View Solutionभुजा a का एक घनाकार ब्लॉक एक चिकने क्षैतिज तल पर वेग v से चल रहा है। बिंदु O पर यह एक मेंड से टकराता है। टकराने के पश्चात ब्लॉक की कोणीय चाल है।
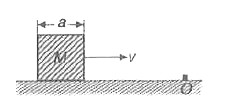
View SolutionA cubical block of side 'a' is moving with velocity v on a smooth horizontal plane. At point O it collides with a bund. The angular speed of the block after collision is
View SolutionIf of of then is
View SolutionA block is drawn on a smooth horizontal plane with a light rope moving with v velocity, as shown in the figure. The horizontal velocity of the block is
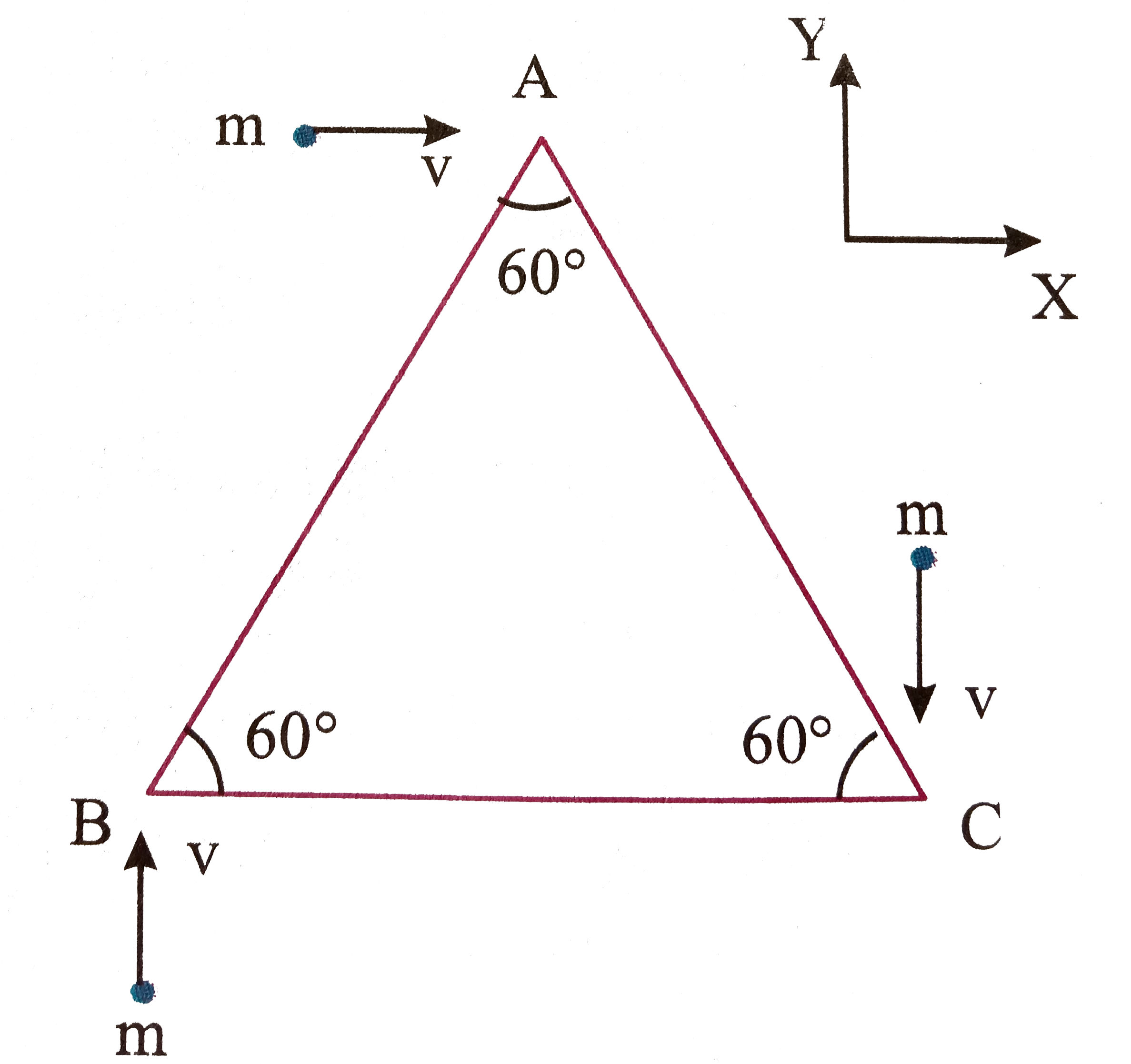
View SolutionA triangular block of mass and side lies on a smooth horizontal plane is shown. There point masses of the each strikes the block at and with speed as shown. After the collision the particle come to rest. Then
View SolutionA block is dragged on a smooth plane with the help of a rope which moves with velocity v as shown in figure. The horizontal velocity of the block is

View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :
View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :
View SolutionA block is pulled on a smooth plane by a rope moving with a velocity v as shown in the figure. The horizontal velocity of the block will be-
View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :

View SolutionA block is pulled on a smooth horizontal plane with the help of a light rope which moves with velocity v as shown in the figure. The horizontal velocity of the block is:
View Solution