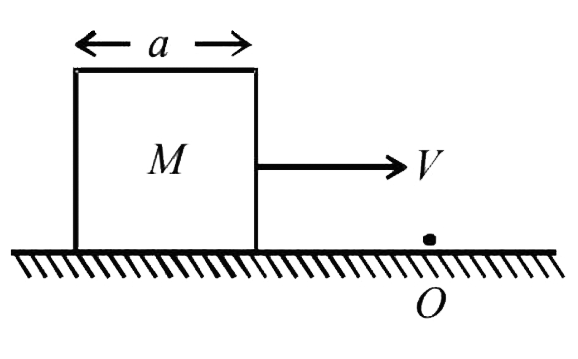
A cubical block of side a is moving with velocity v on a horizontal smooth palne as shown . It hits a ridge at point O. The angular sped of the block after it hits O is
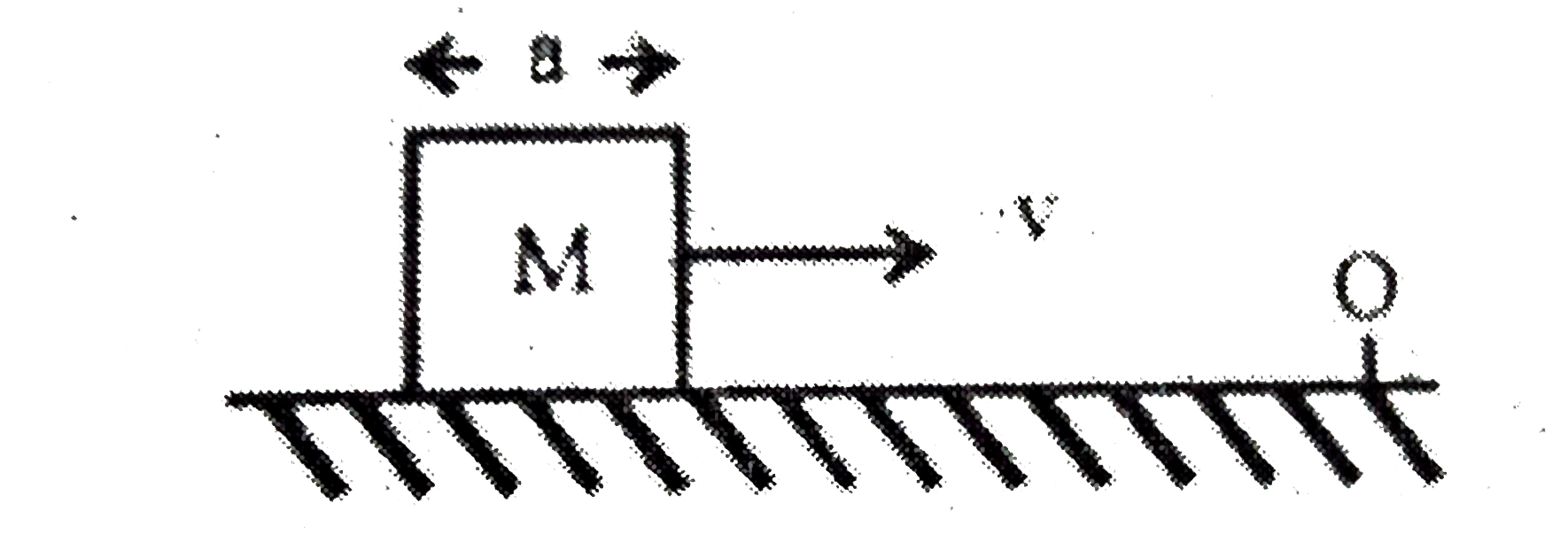
3v/2a
√3v/√2a
3v/4a
Zero
The correct Answer is:C
Angular momentum with respect O before colliding with O=Mva2
On collision , the block will rotate about the side passing through O.
By law of conservation of angular momentum
Mva2=lω
⇒Mva2=(Ma26+Ma22)ω⇒ω=3v4a
Where I is the axis perpendicular to the plane passing through O.
Topper's Solved these Questions
Similar Questions
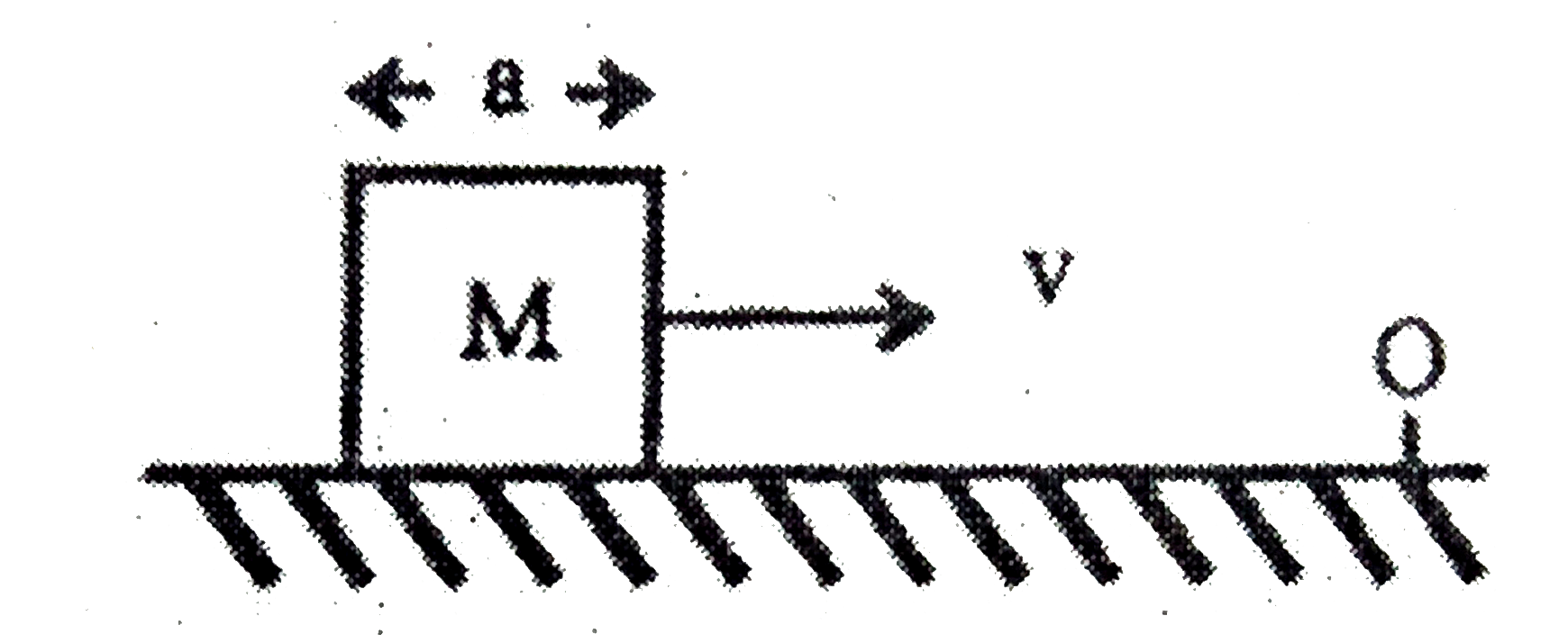
A cubical block of side a is moving with velocity v on a horizontal smooth plane as shown. It hits a ridge at point O. The angular speed of the block after it hits O is:
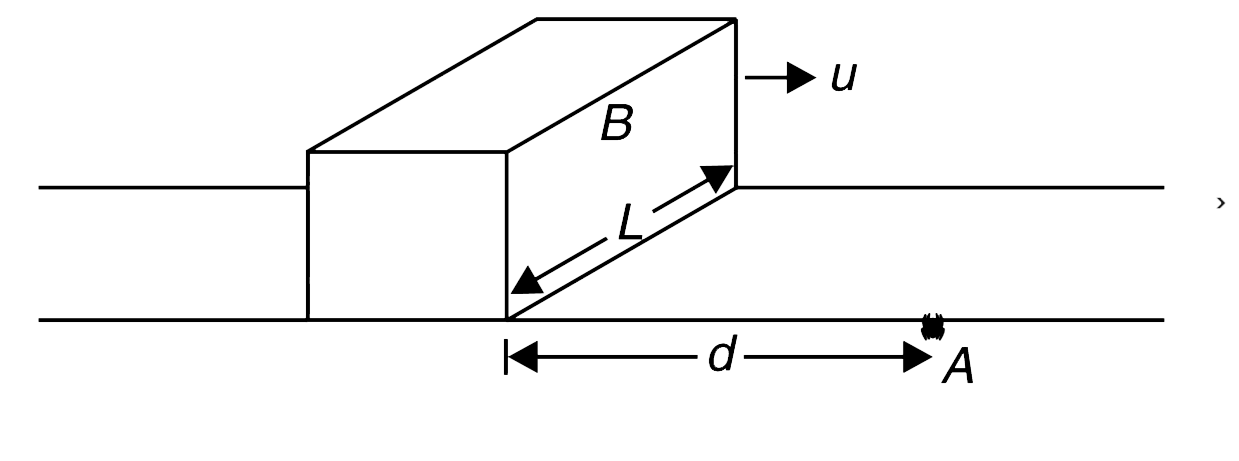
View SolutionA heavy block 'B' is sliding with constant velocity u on a horizontal table. The width of the block is L. There is an insect A at a distance d from the block as shown in the figure. The insect wants to cross to the opposite side of the table. It begins to crawl at a constant velocity v at the instant shown in the figure. Find the least value of v for which the insect can cross to the other side without getting hit by the block.
View Solution
Knowledge Check
A cubical block of side a is moving with velocity v on a horizontal smooth plane as shown. It hits a ridge at point O. The angular speed of the block after it hits O is:
 A3v//4aB3v//2aC√3v√2aDZero
A3v//4aB3v//2aC√3v√2aDZeroA cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed fo the block after it hits O is
 A3V4aB3V2aC√3V√2aDzero
A3V4aB3V2aC√3V√2aDzeroA cubical block of side a is moving with velocity v on a horizontal smooth plane as shown. It hits a ridge at point O. The angular speed of the block after it hits O is:
 A3v/4aB3v/2aC√3v/√2aDZreo
A3v/4aB3v/2aC√3v/√2aDZreo
A heavy block B is sliding with constant velocity u=5m/s on a horizontal table. The width of the block is L=4m.
There is an insect A at distance d=3m from the block as shown in the figure. The insect wants to cross to the oposite side of the table. It begins to crawl at a constant velocity v at the instant shown in the figure. Find the least value of v (in m/s) for which the insect can cross to the other side without getting hit by the block.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

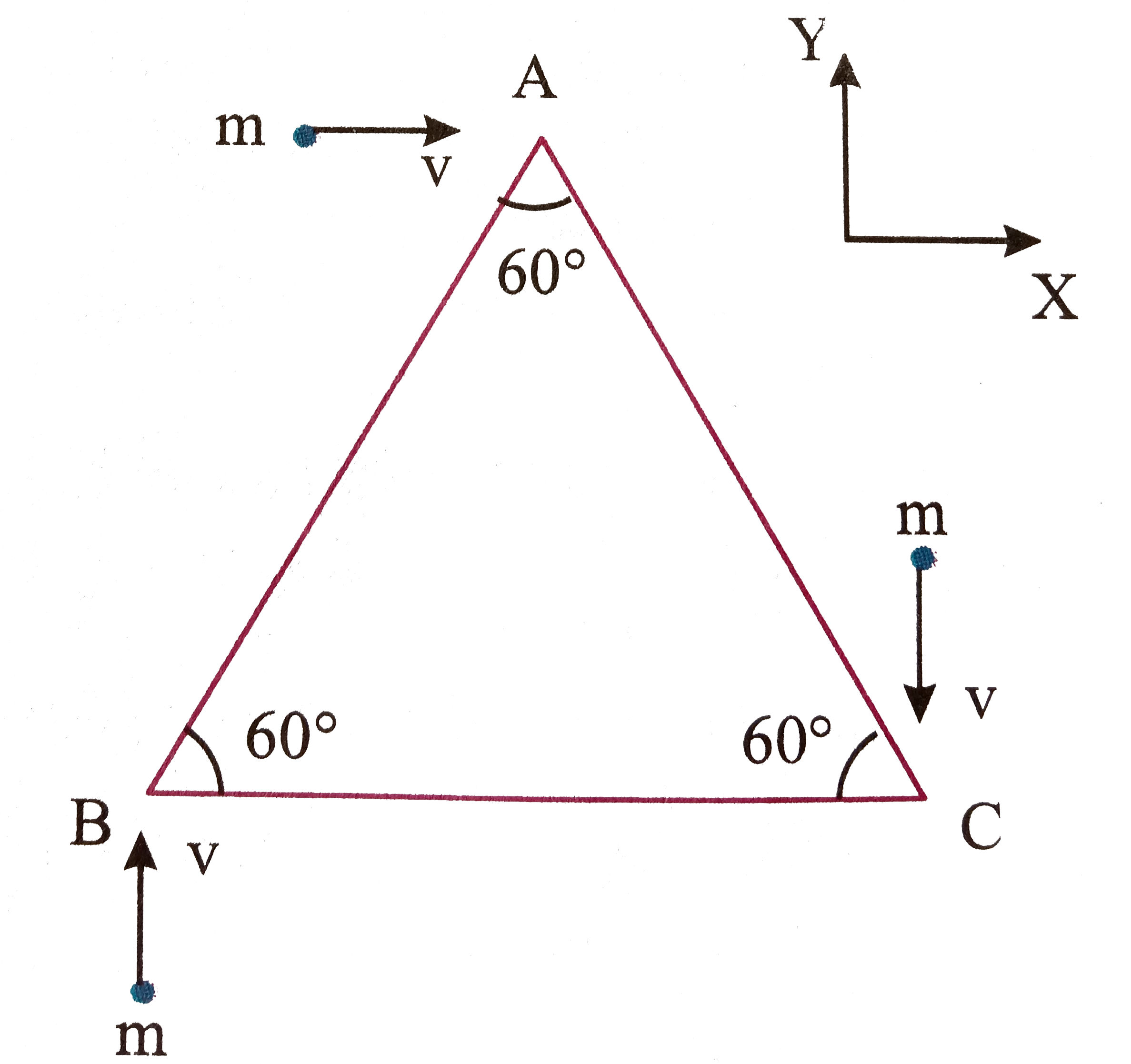
View SolutionA triangular block ABC of mass m and side 2a lies on a smooth horizontal plane is shown. There point masses of the m each strikes the block at A,B and C with speed as shown. After the collision the particle come to rest. Then
View Solution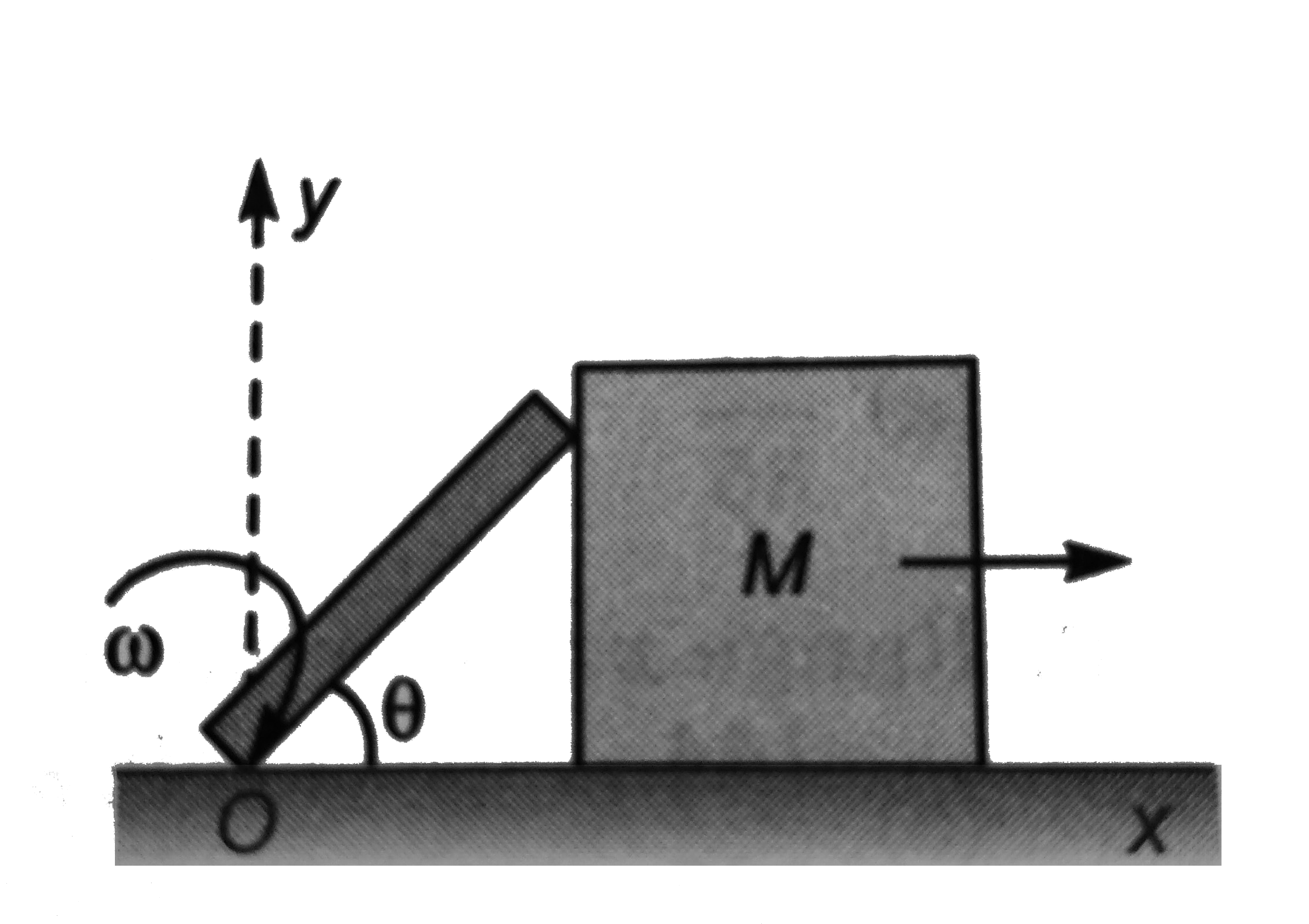
A uniform rod of mass m and length l is applied pivoted at point O. The rod is initially in vertical position and touching a block of mass M which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point O this causes the block to move forward as shown The rod loses contact with the block at θ=30∘ all surfaces are smooth now answer the following questions.
Q. The velocity of block when the rod loses contact with the block is
View Solution
