Co-efficient of xr is denoted by ar in expansion of x+1p+q thena ap = aq b ap = -aq c ap aq = +1 d None
Correct option: a ap = aq Explanation:Tr+1 = ncr an–r br given x + 1p+q ∴ Tr+1 = p+qcr ∙ xp+q–r ∙ 1r Tr+1 = p+qcr ∙ xp+q–r 1given: coefficient of xr = ar First to find coefficient of xp.we will put q = r∴ T1 = p+qcr ∙ xp ------ from 1∴ coefficient of xp = p+qcr ∴ ap = p+qcr 2similarly coefficient of xq is obtained by putting p = r∴ from 1T2 = q+pcr xq ∴ coefficient of xq = q+pcr i.e. aq = q+pcr 3from 2 & 3ap = q+pcr aq = p+qcr ∴ ap = aq
Related Solutions
AB is the diameter of a semi-circle.Through A draw any straight lines AP,AQ meet the circumference again at P and Q. Draw PM,QN perpendicular to AB. Then the ratio AM:AN is equal to (A) BP^(2):BQ^(2) (B) AP^(2):AQ^(2) (C) AP^(2):AQ^(2) (C) AP^(2):AQ^(2) (C) AP^(2):AQ^(2) (D) none of these
View SolutionIn Fig.12.126,AP perp L and PR>PQ Show that AR>AQ
View SolutionIn the given figure, is a rectangle in which segments and are drawn as shown. Then the length of is
View SolutionO AP and AQ are two tangents to the central circle. If the radius of the circle is 9 cm and OA = 15 cm AP+AQ = ?
View SolutionK_(ap) in the positions of A_3B_((aq)) is the solubility for:
View SolutionIn the given figure, prove that .
View SolutionAP and AQ are tangent drawn from a ponit A to a circle with centre O and radius 9cm. If OA = 15 cm. then AP + AQ = …….. Cm.
View SolutionD and E are the mid-points of AB and AC respectively of the AP is the median of BC. AP intersects DE at Q. Prove that DQ = QE and AQ = QP.
View SolutionAssertion : In DeltaABC, E and F are the midpoints of AC and AB respectively. The altitude AP at BC intersects FE at Q. Then, AQ = QP. Reason : Q is the midpoint of AP.
View SolutionIn Fig. 10.83, if , then (FIGURE) (b) (c) (d)
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View Solutionनिचे की आकृति में साबित करे की
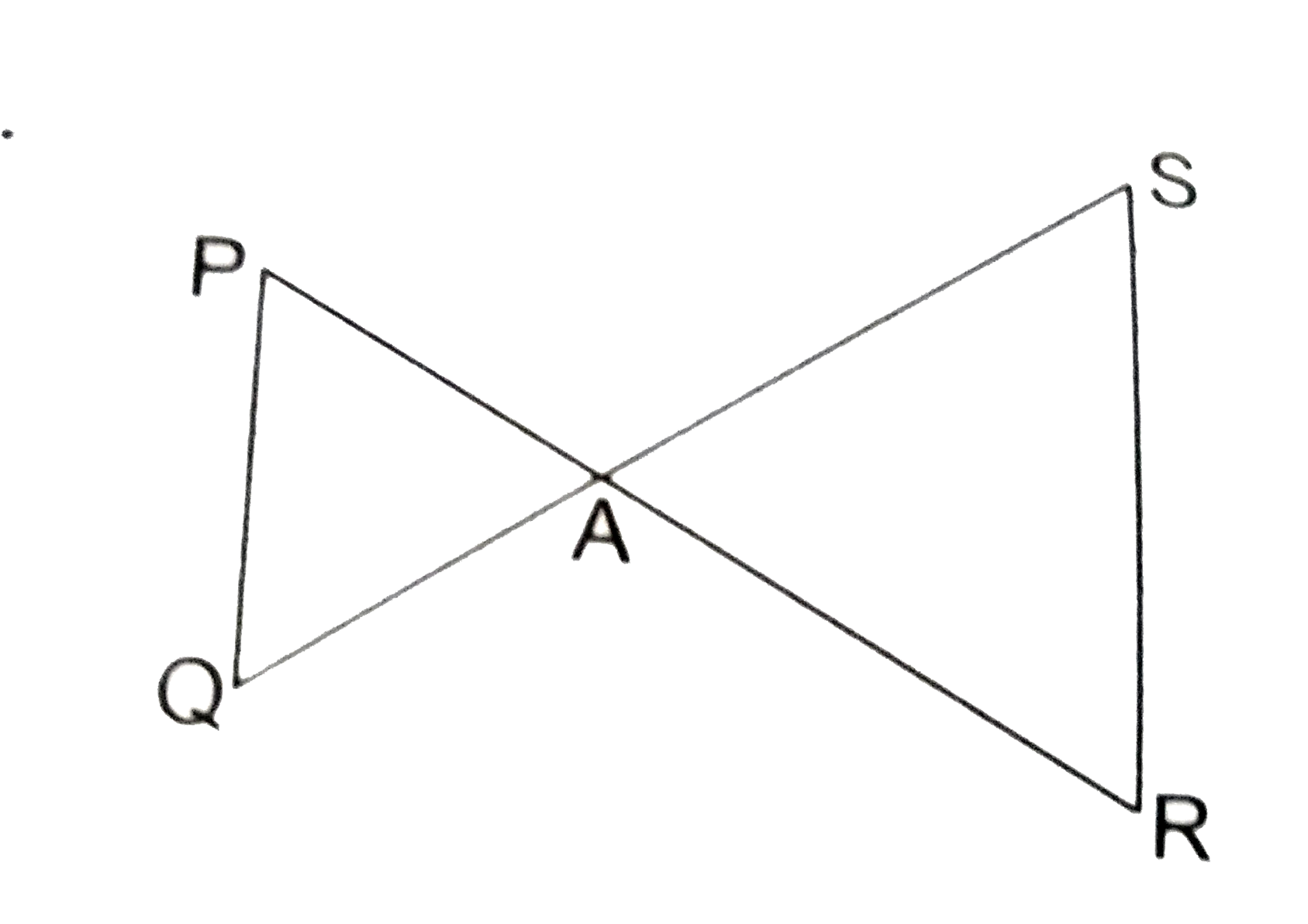
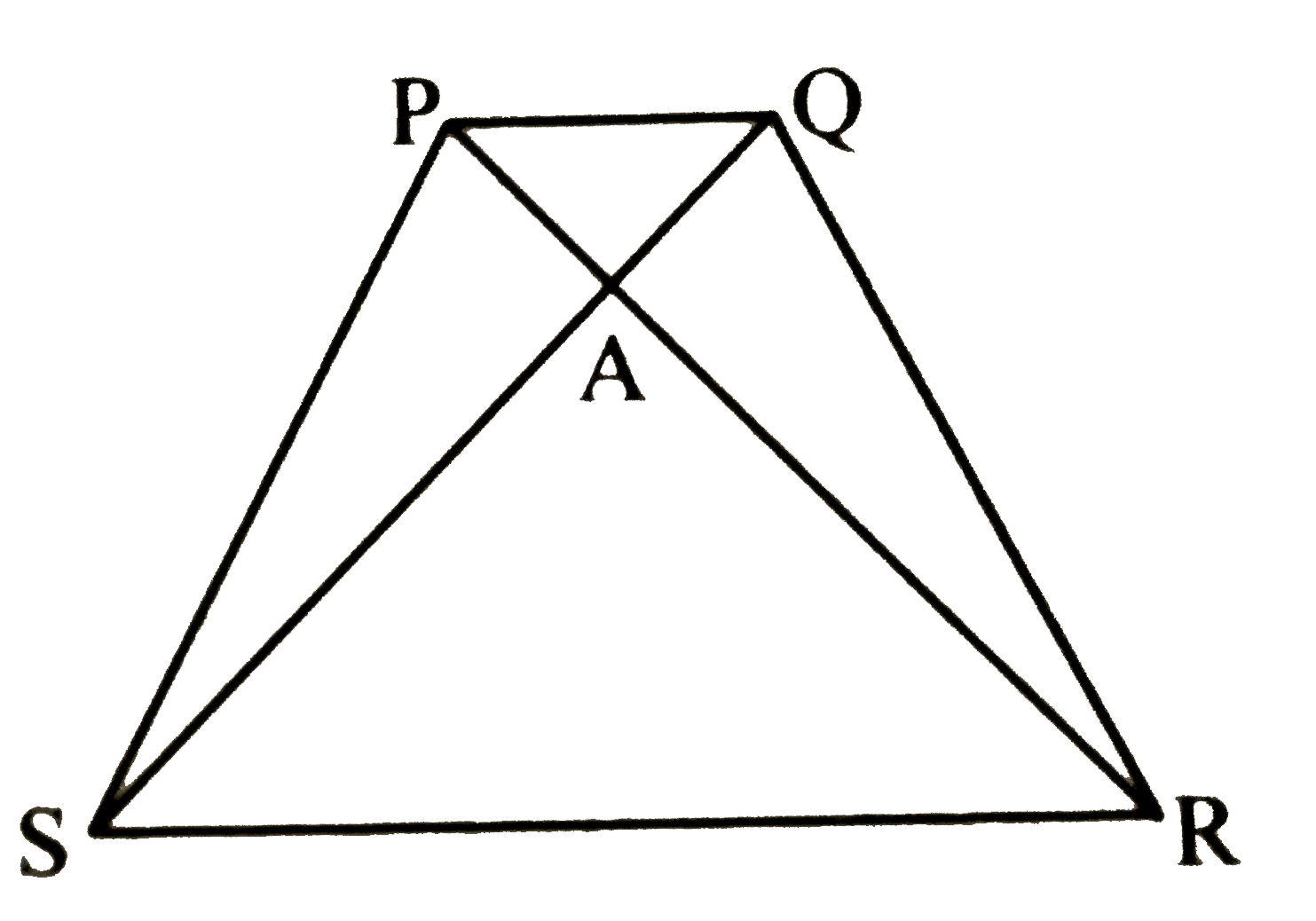
View SolutionGiven : In trapezium PQRS, side PQSR, AR = 5 AP, AS = 5 AQ, then prove that SR=5 PQ.
View SolutionIn Fig.
 ,
,
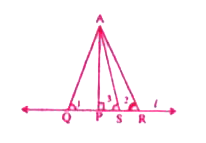
AP is the shortest line-segment that can be drawn from A to the line . If , prove that .
View Solutionयदि हो, तथा हो, तो सिध्द करो कि .
View Solutionসঠিক উত্তরটি নির্বাচন করো : যদি হয়, তবে = ?
View SolutionIn Fig.
 , AP is the shortest line-segment that can be drawn from A to the line . If , prove that .
, AP is the shortest line-segment that can be drawn from A to the line . If , prove that .
View SolutionA point A is inside a triangle PQR. Show that .
View SolutionGiven : In trapezium PQRS, side PQSR, AR = 5 AP, AS = 5 AQ, then prove that SR=5 PQ.

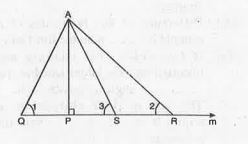
View SolutionIn ,AQ is the bisector of . ,,If AP is the bisector of What is ?
View Solution