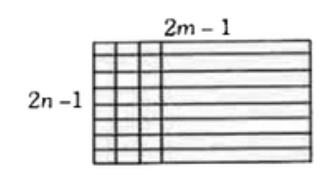
A rectangle with sides 2m-1 and 2n-1 is divided into squares of unit length by drawing Parallel lines as shown in the diagram then the no. of rectangles possible with odd side length is _______a mnm+1n+1 b m2n2 c m+n+12d 4m+n-1
Correct option: b m2n2Explanation:Number of ways of selecting verticle sides= 1 + 3 + 5 + .....+ 2n - 1 = n2 Number of ways of selecting horizontal sides= m2 ∴ Number of rectangles = m2n2
Related Solutions
A rectangle with sides (2m-1) and (2n -1) is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side lengths is :

View SolutionA rectangle with sides of lengths units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) (b) (c) (d) non of these
View SolutionA rectangle with sides of lengths units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) (b) (c) (d) non of these
View SolutionA rectangle with sides of lengths units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) (b) (c) (d) non of these
View SolutionA rectangle with sides of lengths units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) (b) (c) (d) non of these
View SolutionA rectangle with sides of lengths (2n-1) and (2m-1) units is divided into squares of unit length.The number of rectangles which can be formed with sides of odd length,is (a) m^(2)n^(2) (b) mn(m+1)(n+1) (c) 4^(m+n-1) (d) non of these
View Solutionभुजाओं 2m – 1 और 2n – 1 वाले एक आयत को इकाई लंबाई के वर्गों में विभाजित किया गया है। विषम लंबाई की दोनों भुजाओं से बनाये जा सकने वाले आयतों की संख्या है:
View SolutionA rectangle with sides 2m-1 and 2n-1 divided into squares of unit length the number of rectangles which can be formed with sides of odd length is
View SolutionA rectangle with sides of lengths (2 n-1) and (2 m-1) units is divided into squares of unit lengths. The number of rectangles which can be formed with sides of odd length is
View Solutionएक आयताकार पट्टी की विमा (2m -1) x (2n -1) है, (जहाँ m 0,n0). इसे भुजाओं के लम्बवत् रेखायें खींचकर इकाई क्षेत्रफल के वर्गों में विभाजित किया जाता है तब उन आयतों की संख्या, जिनकी भुजायें विषम इकाई लम्बाई की हैं, होगी
View SolutionThere is a rectangular sheet of dimension , (where ) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionThere is a rectangular sheet of dimension , (where ) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionThere is a rectangular sheet of dimension , (where ) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionThere is a rectangular sheet of dimensions ( (where It has been divided into squares of unit area by drawing lines perpendicular to the sides. Find number of rectangles having sides of odd unit length.
View SolutionThere is a rectangular sheet of dimension , (where ) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionA rectangle with sides of lengths 15 and 13 unitsis divided into squares of sides of unit length. Thennumber of rectangles which can be formed with thesides of odd length, is
View Solutionएक वर्गाकार शीट का आकार (जहाँ ) है इसकी भुजाओं पर लम्ब रेखाएँ खींचकर इसे इकाई क्षेत्रफल के वर्गों में विभाजित किया जाता है । विषम इकाई लम्बाई वाली भजौं के आयतों की संख्या है -
View SolutionIf m parallel lines in a plane are intersected by a family of n parallel lines, the number of parallelograms that can be formed is a. 1/4m n(m-1)(n-1) b. 1/4m n(m-1)(n-1) c. 1/4m^2n^2 d. none of these
View Solutionएक वर्ग और एक आयत के क्षेत्रफल बराबर हैं। यदि आयत की एक भुजा की लम्बाई संख्यात्मक रूप से वर्ग की एक भुजा की लम्बाई के वर्ग के बराबर है, तो आयत की अन्य ( दूसरी ) भुजा की लम्बाई होगी
View SolutionIf parallel lines in a plane are intersected by a family of parallel lines, the number of parallelograms that can be formed is a. b. c. d. none of these
View Solution