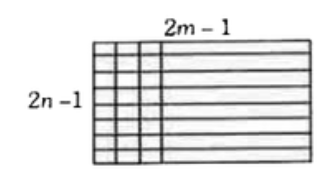
A rectangle with sides of lengths (2 n-1) and (2 m-1) units is divided into squares of unit lengths. The number of rectangles which can be formed with sides of odd length isSolution in Kannada
1: m2n2
2: mn(m+1)(n+1)
3: 4a+a−1
4: none of these
The correct Answer is:A
Step by step video, text & image solution for A rectangle with sides of lengths (2 n-1) and (2 m-1) units is divided into squares of unit lengths. The number of rectangles which can be formed with sides of odd length is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Vertex of the parabola y2−8x−4y+4=0 at
View SolutionOut of 30 consecutive numbers, 2 are chosen at random. The probability that their sum is odd, is
View SolutionA rectangle with sides of lengths (2n-1) and (2m-1) units is divided into squares of unit length.The number of rectangles which can be formed with sides of odd length,is (a) m^(2)n^(2) (b) mn(m+1)(n+1) (c) 4^(m+n-1) (d) non of these
View SolutionA rectangle with sides of lengths 15 and 13 unitsis divided into squares of sides of unit length. Thennumber of rectangles which can be formed with thesides of odd length, is
View Solutionएक आयताकार पट्टी की विमा (2m -1) x (2n -1) है, (जहाँ m> 0,n>0). इसे भुजाओं के लम्बवत् रेखायें खींचकर इकाई क्षेत्रफल के वर्गों में विभाजित किया जाता है तब उन आयतों की संख्या, जिनकी भुजायें विषम इकाई लम्बाई की हैं, होगी
View SolutionA rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these
View SolutionA rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these
View SolutionThe are of a square is the same as that of a rectangle. If the side of a square is 60 m and the breadth of the rectangle is 48 m, find the length of the rectangle.
View Solutionभुजाओं 2m – 1 और 2n – 1 वाले एक आयत को इकाई लंबाई के वर्गों में विभाजित किया गया है। विषम लंबाई की दोनों भुजाओं से बनाये जा सकने वाले आयतों की संख्या है:
View SolutionThere is a rectangular sheet of dimension (2m−1)×(2n−1), (where m>0,n>0) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionA rectangle with sides 2m-1 and 2n-1 divided into squares of unit length the number of rectangles which can be formed with sides of odd length is
View SolutionThe area of a rectangle is 12 square- metre and the length of one side is 34. metre. What is the length of the other side?
View SolutionA rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these
View SolutionThere is a rectangular sheet of dimension (2m−1)×(2n−1), (where m>0,n>0) It has been divided into square of unit area by drawing line perpendicular to the sides. Find the number of rectangles having sides of odd unit length.
View SolutionA rectangle with sides of lengths (2n−1)and(2m−1) units is divided into squares of unit length. The number of rectangles which can be formed with sides of odd length, is (a) m2n2 (b) mn(m+1)(n+1) (c) 4m+n−1 (d) non of these
View Solution
