What can be said about the center of mass of a uniform hemisphere without making any calculation? Will its distance from the center be more than r/2 or less than r/2?
Less than r/2. Just visualize a uniform cylinder of radius r and height r. Its center of mass will be at r/2 from the center of the base circle. Since the given hemisphere can be made by carving out masses from the upper parts the center of mass of the remaining hemisphere will be less than r/2.
Related Solutions
What can be said about the centre of mass of a uniform hemisphere without making any calculation? Will its distance from the centre be more than r/2 or less than r/2?
View SolutionWhat can be said about the centre of mass of a uniform hemisphere without making any calculation? Will its distance from the centre be more than r/2 or less than r/2?
View SolutionWhat can be said about the centre of mass of a solid hemisphere of radius r without making any calculation. Will its distance from the centre be more than r//2 or less than r//2 ?
View SolutionWhat can be said about the centre of mass of a solid hemisphere of radius r without making any calculation. Will its distance from the centre be more than r//2 or less than r//2 ?
View SolutionWhat can be said about the centre of mass f a uniform hemisphere without making any calculation? Wil its distance from the centre be more thn r/2 or less than r/2?
View Solutionएक अक्स्मान धनत्व की गोलाकार वस्तु के द्रव्यमान केंद्र की स्थिति के बारे में बिना कोई गणना किए आप क्या बता सकते है ? क्या यह गोले के केंद्र से R/2 से कम दूरी पर होगा, R/2 दूरी पर होगा, या R/2 दूरी से भी अधिक दूरी पर होगा ?
View SolutionThe distance of its center of mass from the center of a hemispherical shell of radius R is-
View SolutionThe distance of the center of mass of a uniform semicircular wire of radius R from its geometric center:
View SolutionAll the particles are situated at a distance R from the origin. The distance of centre of mass of the body from the origin will be (1) More than R (2) Less than R (3) Equal to R (4) At the origin
View SolutionAll the particles are situated at a distance R from the origin. The distance of centre of mass of the body from the origin will be (1) More than R (2) Less than R (3) Equal to R (4) At the origin
View SolutionFind moment of inertia of a uniform ring (mass m, radius r) about chord AA' at distance R/2 from center.
View SolutionThe radius of a spherical shell is R and mass M, from its center. R//2 A point mass is located at the distance.
View SolutionTwo solid hemispheres of radii R and with centers O and O' respectively as shown in figure. The density of bigger hemisphere is and that of smaller hemisphere is . Taking center of bigger hemisphere is at origin and the distance between centres of two hemisphere OO' is find co - ordinates of center of mass of the system.
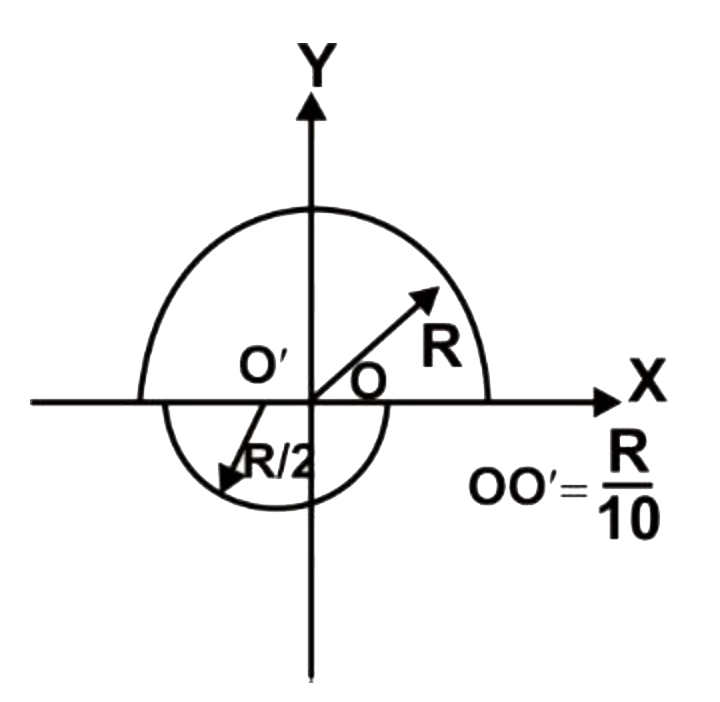
View SolutionTwo solid hemispheres of radii R and with centers O and O' respectively as shown in figure. The density of bigger hemisphere is and that of smaller hemisphere is . Taking center of bigger hemisphere is at origin and the distance between centres of two hemisphere OO' is find co - ordinates of center of mass of the system.

View Solutionबड़ी संख्या में कण केन्द्र के आसपास है प्रत्येक की केन्द्र से दूरी R है। निकाय के केन्द्र से द्रव्यमान केन्द्र की दूरी क्या है
View SolutionAn urban center of more than 11,000 and less than 25,000 inhabitants is classified as
View Solutionद्रव्यमान M और त्रिज्या R के एक ठोस गोले में, त्रिज्या की एक गोलीय गुहिका इस प्रकार बनाई गई है कि गुहिका का केंद्र गोले के केंद्र से से दूरी पर है। एक बिंदु द्रव्यमान m को गोले के केंद्र से की दूरी पर गुहिका के अंदर रखा जाता है। गोले और बिंदु द्रव्यमान m के बीच गुरुत्वाकर्षण खिंचाव है
View Solutionदो द्रव्यमान तथा दूरी पर रखे हों तो उसके द्रव्यमान केंद्र की स्थिति क्या होगी ?
View SolutionA semicircular lamina of mass and radius and centre . Its center of mass is at a distance from . Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
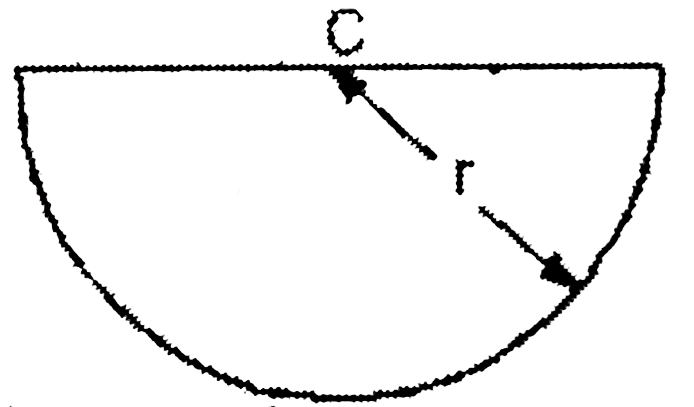
View SolutionA semicircular lamina of mass and radius and centre . Its center of mass is at a distance from . Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:

View Solution